Parameters estimation

Mixture Models in R

Victor Medina

Researcher at The University of Edinburgh

head(data)

         x
1 3.294453
2 5.818586
3 2.380493
4 4.415913
5 5.048659
6 4.750195

Mixture Models in R

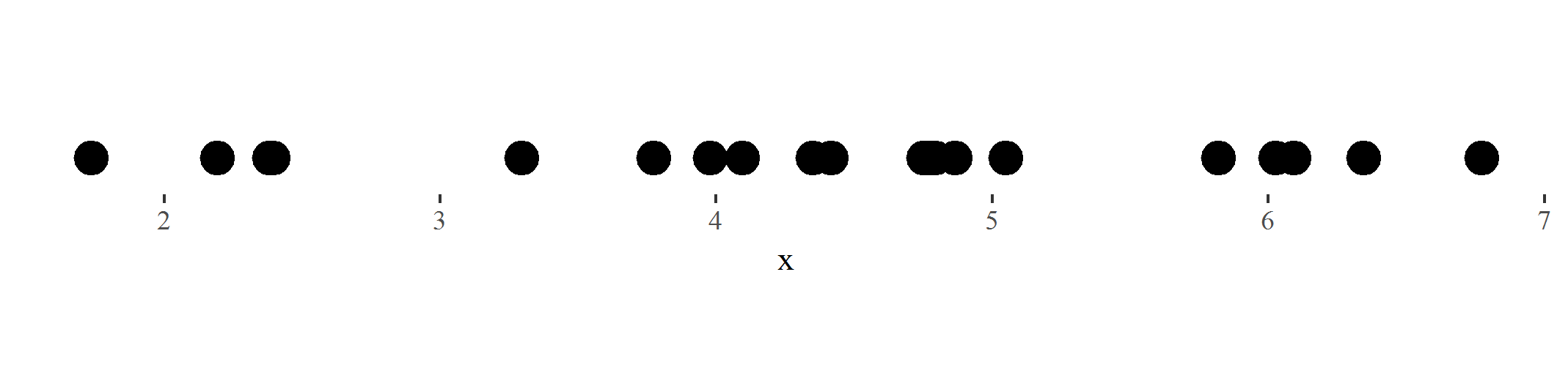
Assumptions

  1. Which distribution? $\rightarrow$ Gaussian distribution $\checkmark$
  2. Number of clusters? $\rightarrow$ 2 clusters $\checkmark$
  3. What parameters?
    • 2 means
    • 2 proportions
    • 2 sd $\rightarrow$ both equal 1 $\checkmark$

$\Rightarrow$ 4 parameters to be estimated! (2 means and 2 proportions)

Mixture Models in R

1 Known probabilities $\rightarrow$

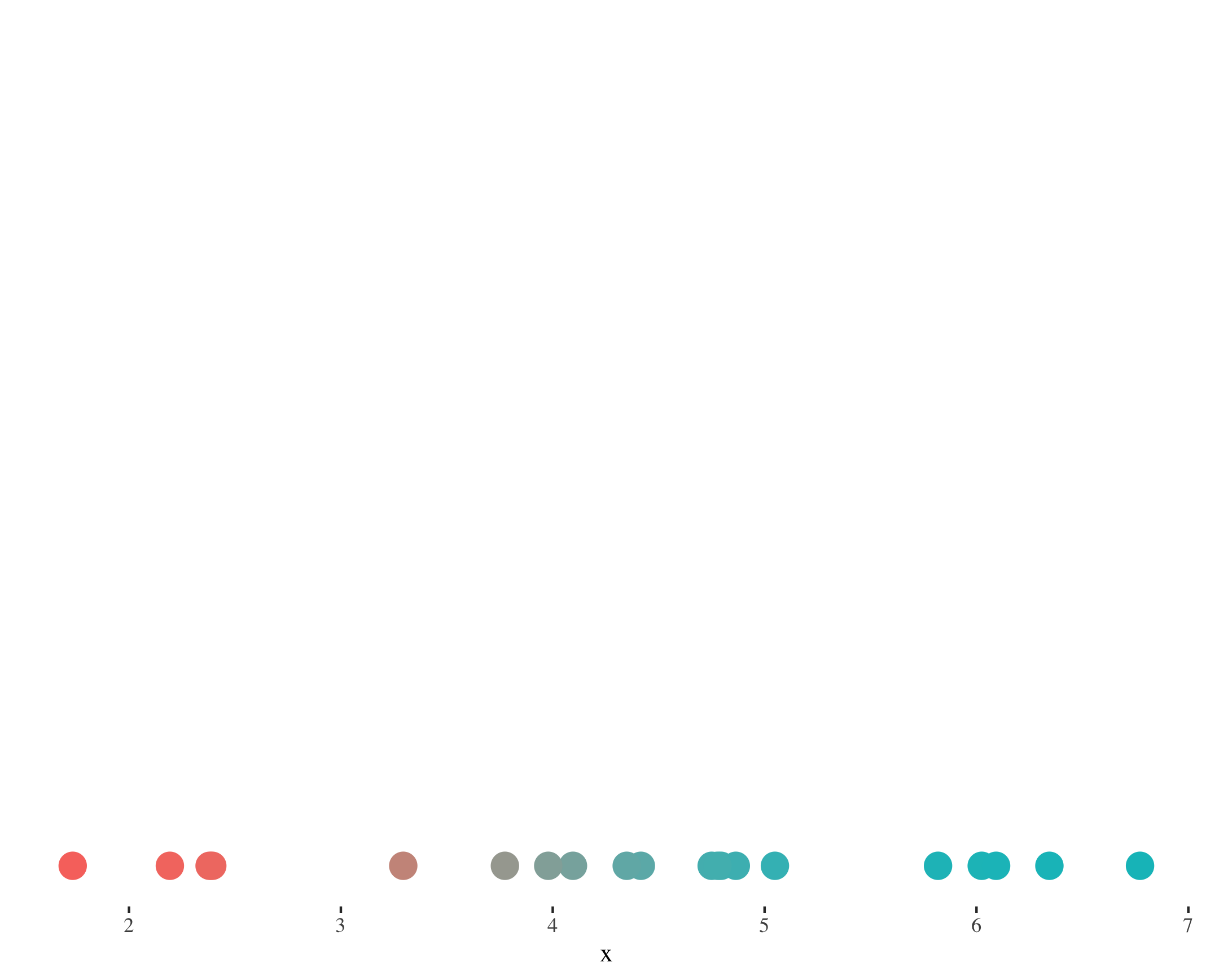
Estimate means and proportions

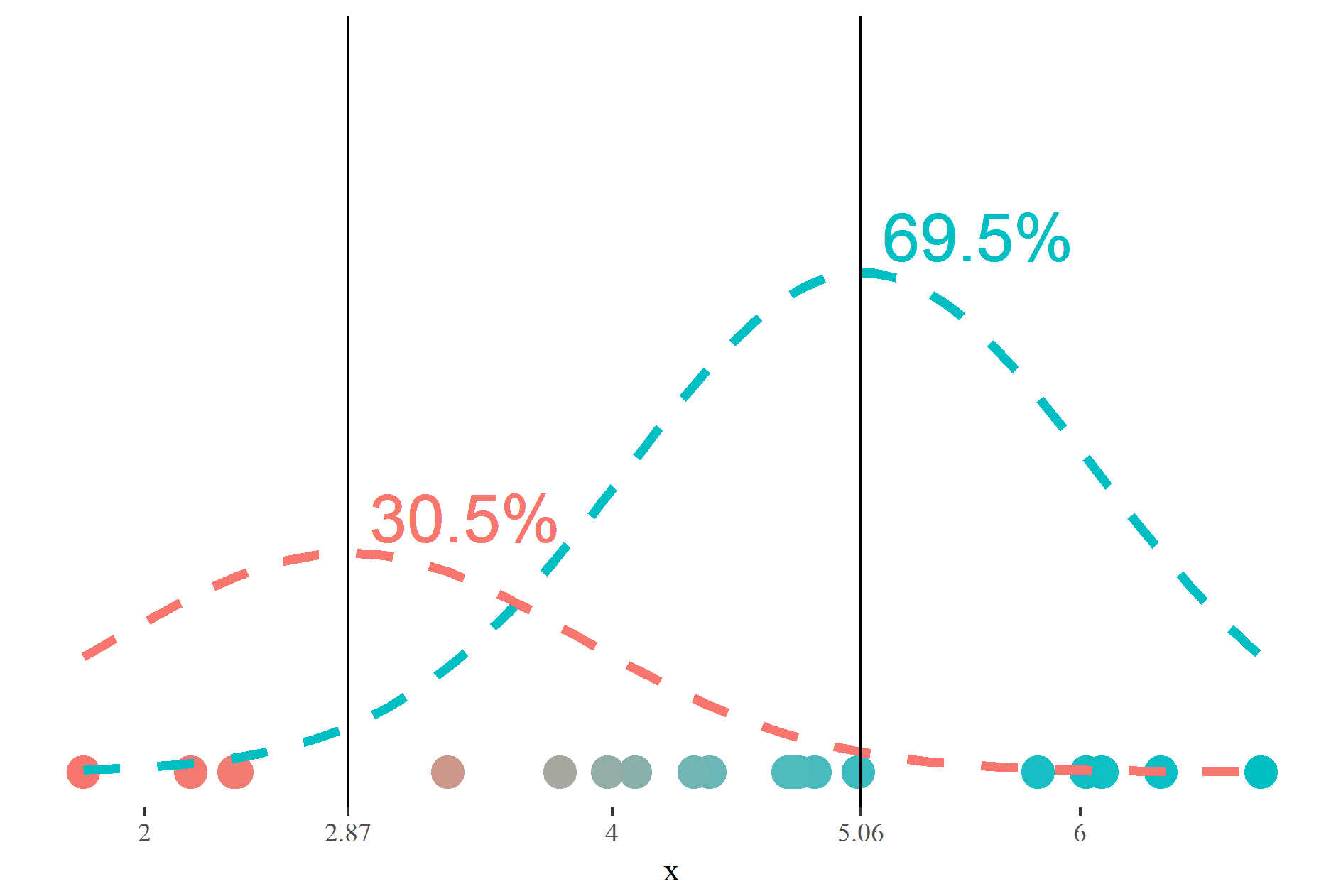
2 Known means and proportions $\rightarrow$

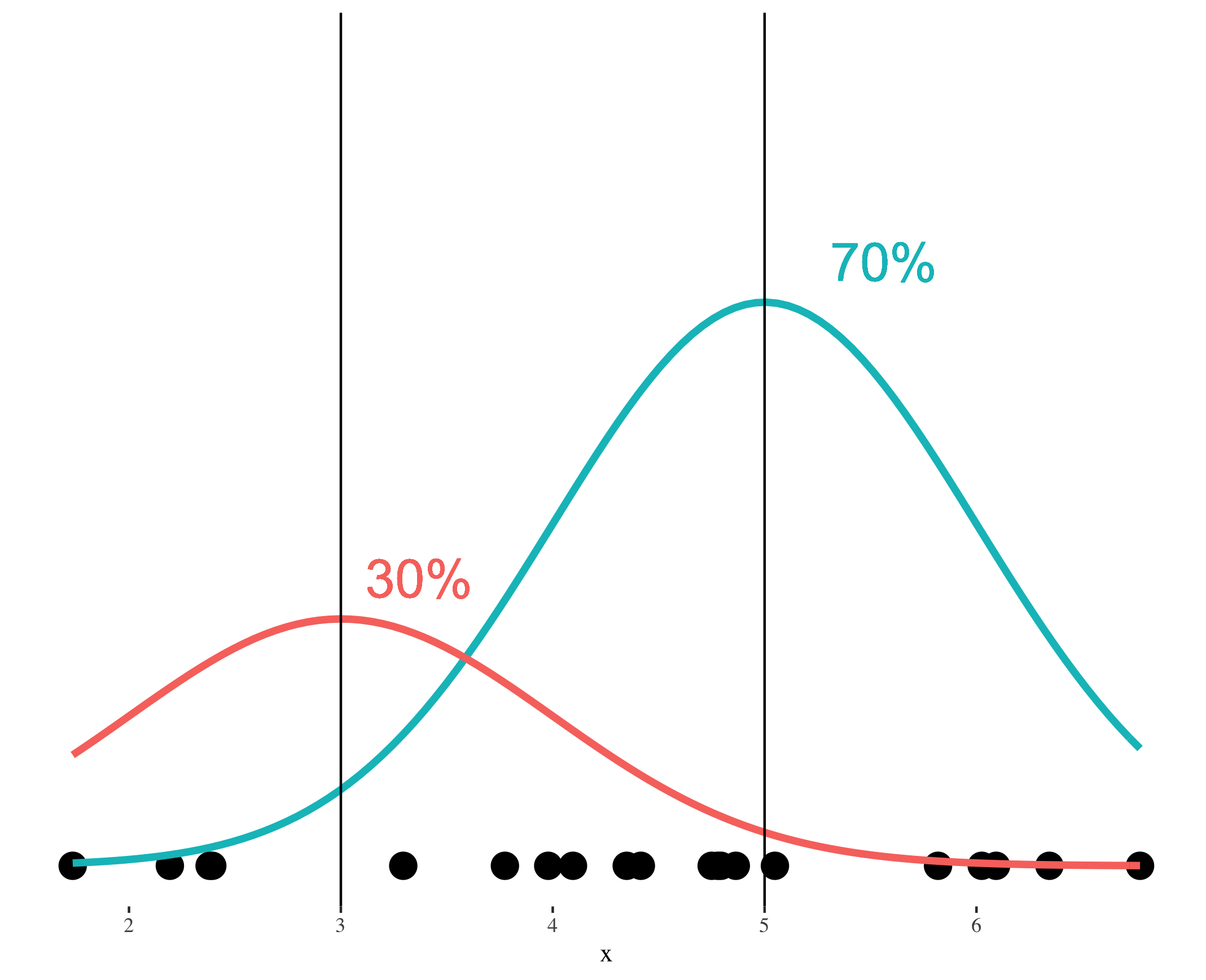
Estimate probabilities

Mixture Models in R

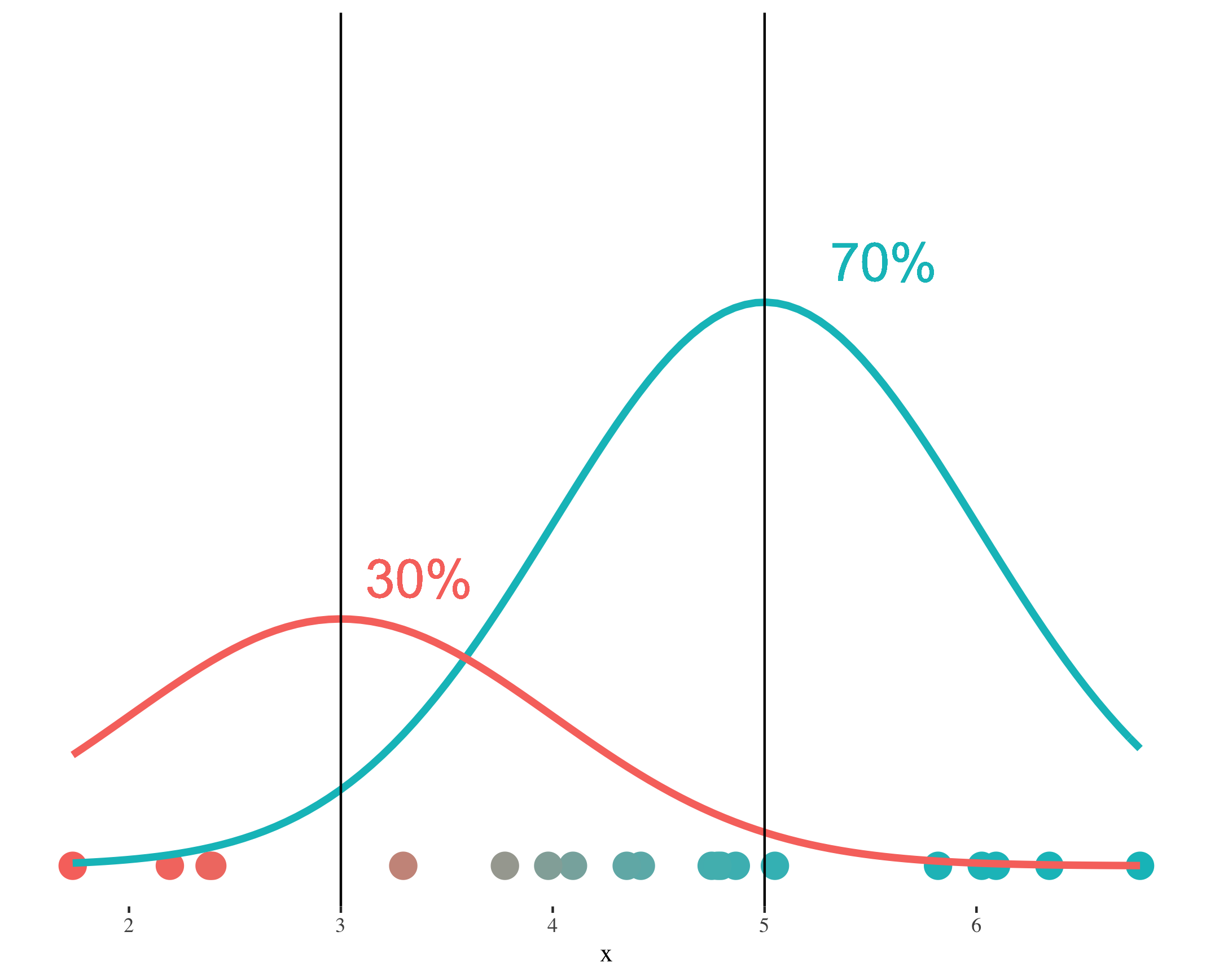
Step 1: Known probabilities

head(data_with_probs)

         x prob_red prob_blue
1 3.294453     0.64      0.36
2 5.818586     0.01      0.99
3 2.380493     0.92      0.08
4 4.415913     0.16      0.84
5 5.048659     0.05      0.95
6 4.750195     0.09      0.91

Mixture Models in R

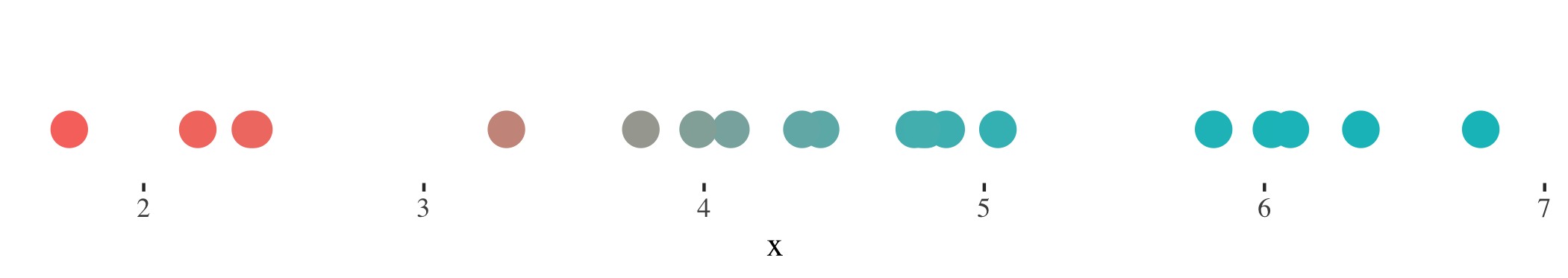
For the means

means_estimates <- data_with_probs %>%
   summarise(mean_red = sum(x * prob_red) / sum(prob_red),
             mean_blue = sum(x * prob_blue) / sum(prob_blue))
means_estimates

  mean_red mean_blue
1  2.86925  5.062976

For the proportions

proportions_estimates <- data_with_probs %>% 
   summarise(proportion_red = mean(prob_red),
             proportion_blue = 1 - proportion_red)
proportions_estimates

  proportion_red proportion_blue
1          0.305           0.695
Mixture Models in R

Mixture Models in R

Step 2: Known means and proportions

Mixture Models in R

Mixture Models in R

Mixture Models in R

Mixture Models in R

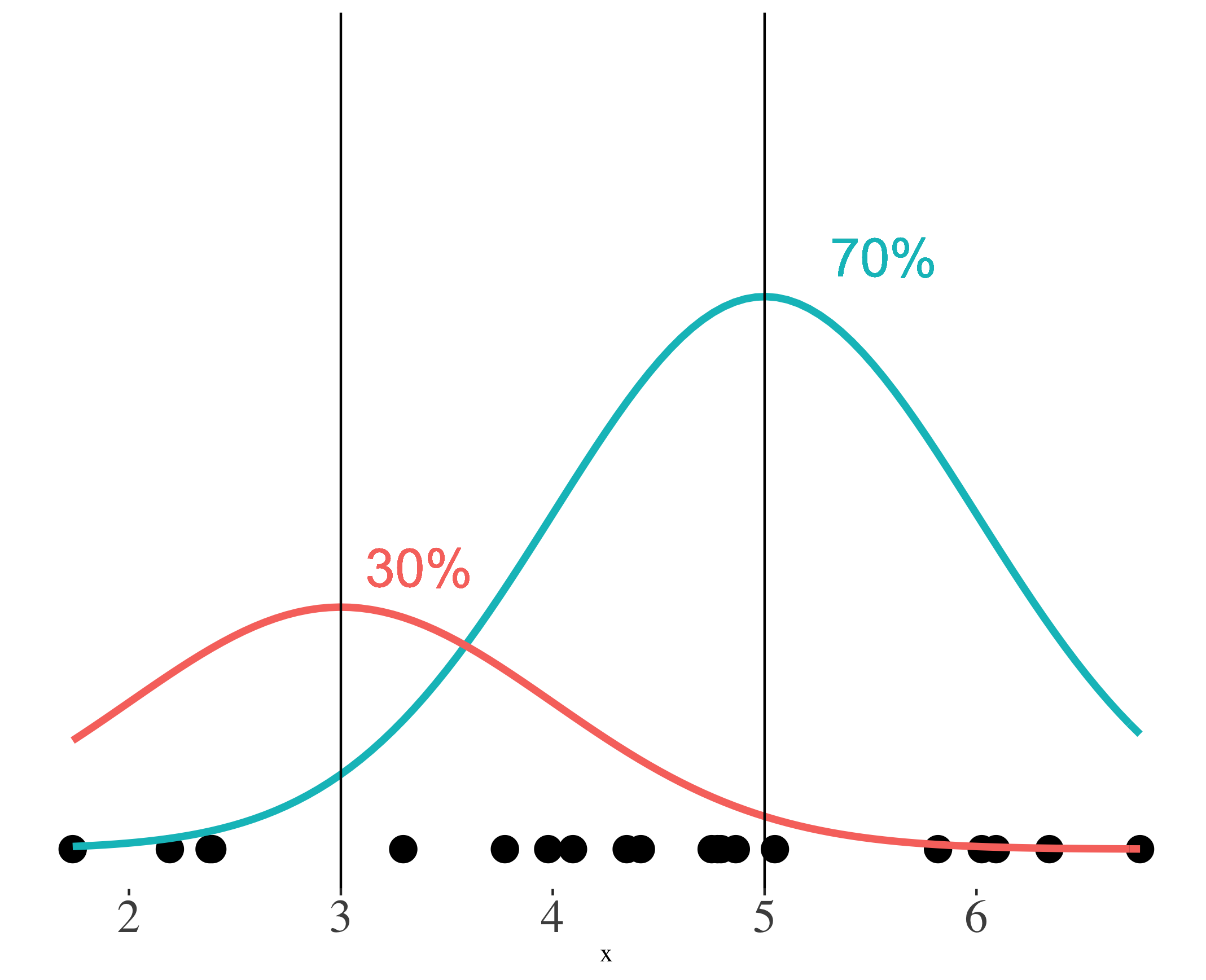
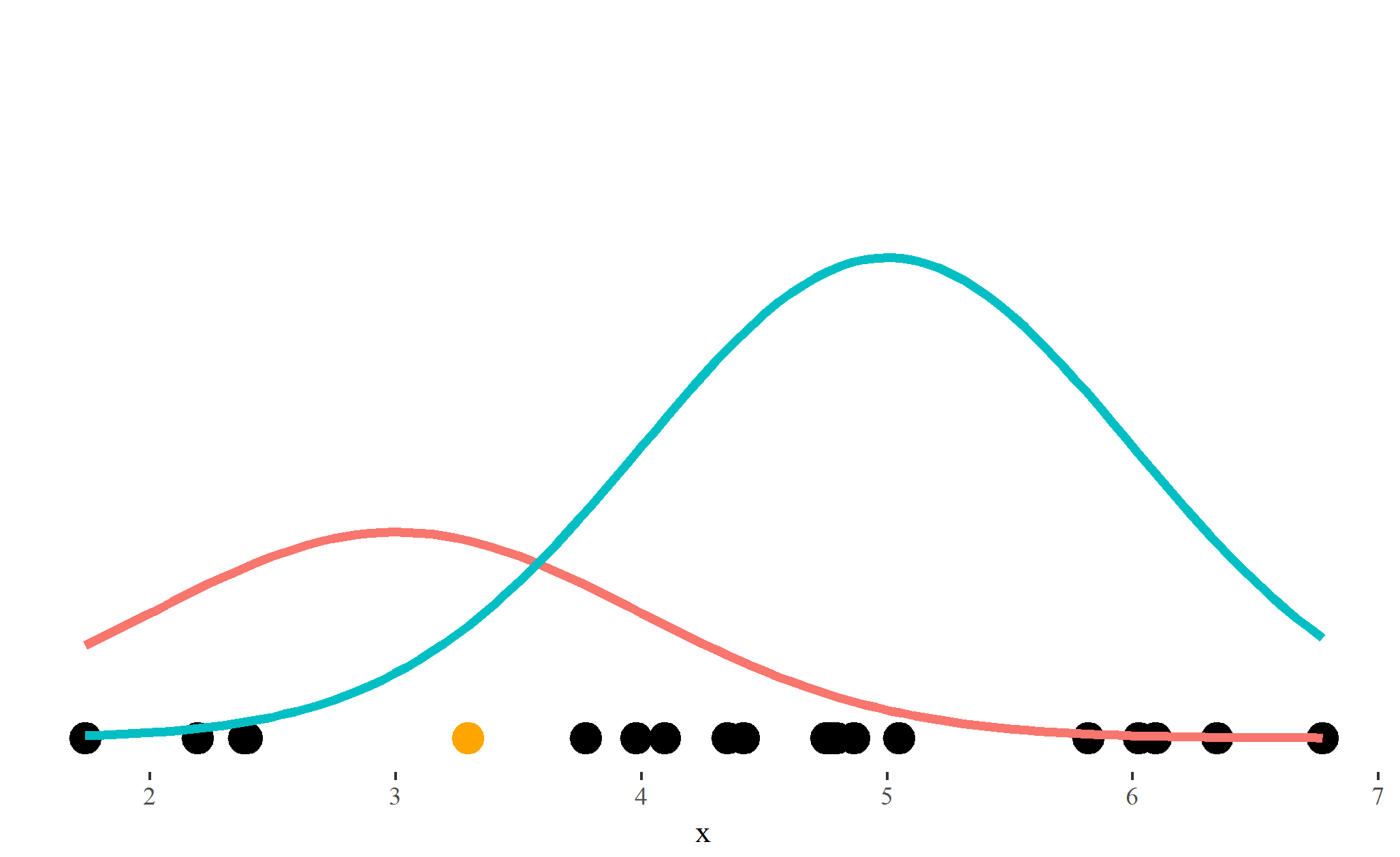
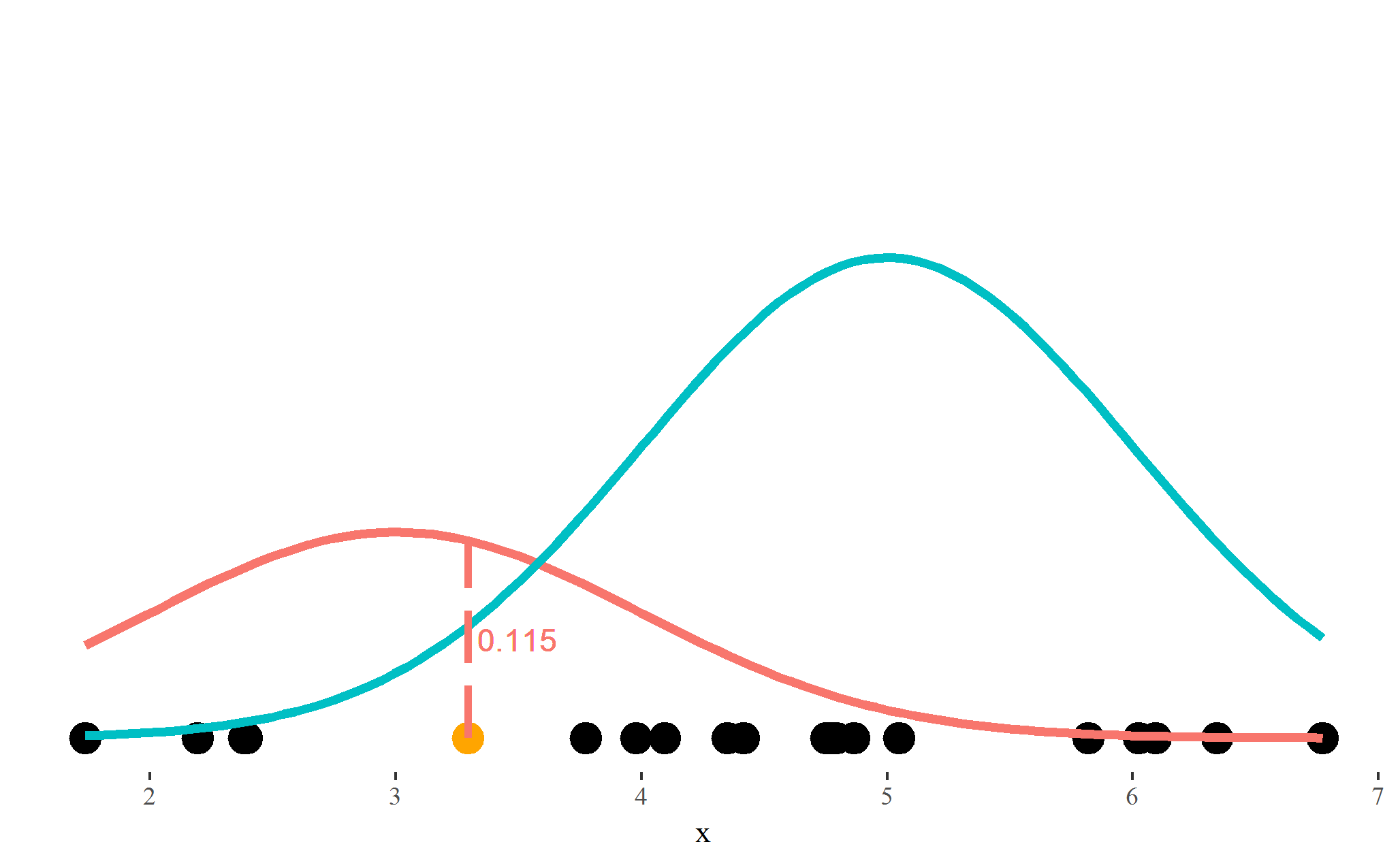
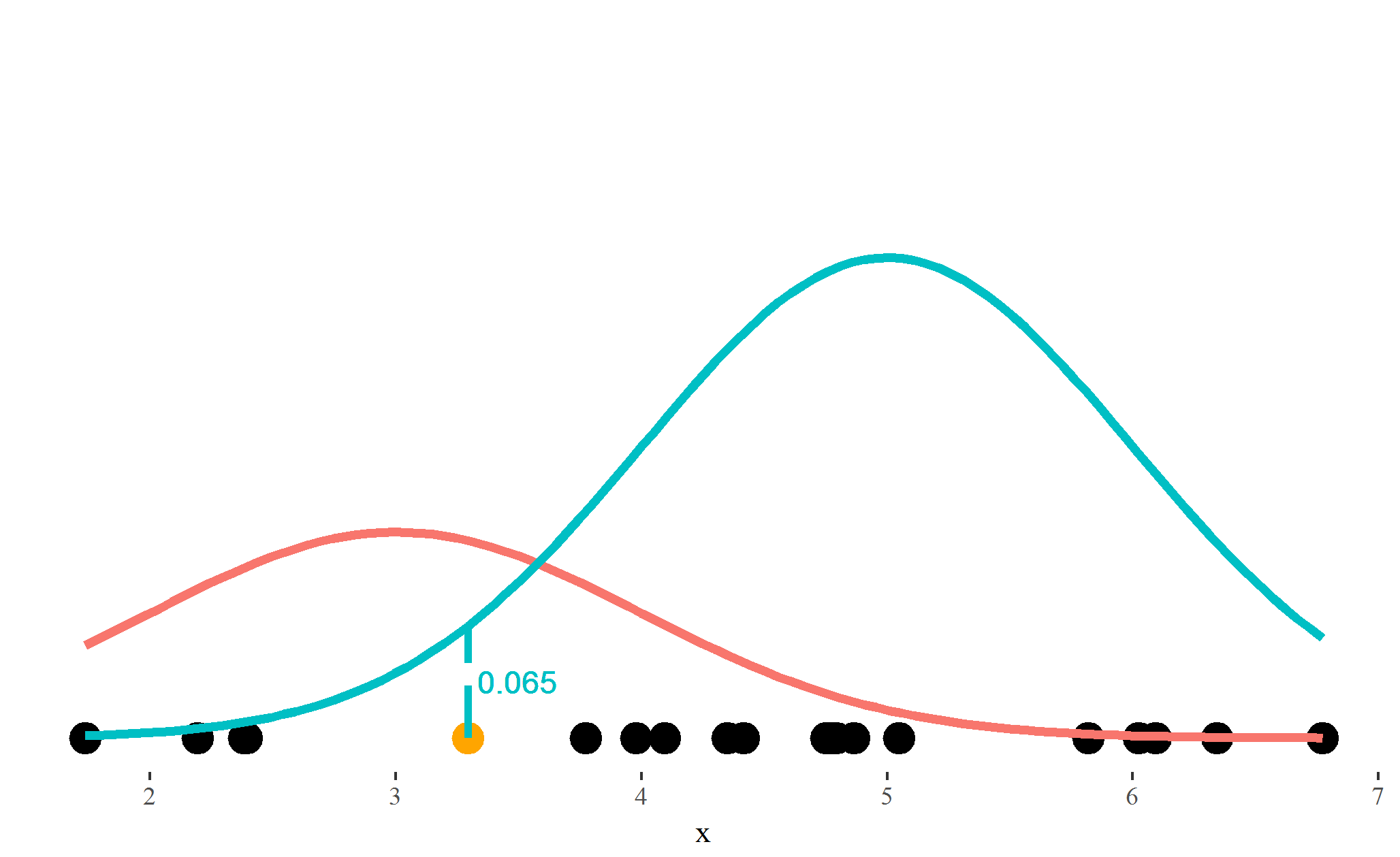
Step 2: Scaled probabilities

$\text{Probability}_{\text{ blue}}=\frac{0.065}{0.115 + 0.065}=0.36$

data %>% 
   mutate(prob_from_red = 0.3 * dnorm(x, mean = 3),
          prob_from_blue = 0.7 * dnorm(x,mean = 5),
          prob_red = prob_from_red/(prob_from_red + prob_from_blue),
          prob_blue = prob_from_blue/(prob_from_red + prob_from_blue)) %>% 
   select(x, prob_red, prob_blue) %>% head(4)

         x   prob_red  prob_blue
1 3.294453 0.63733037 0.36266963
2 5.818586 0.01115698 0.98884302
3 2.380493 0.91619343 0.08380657
4 4.415913 0.15721146 0.84278854
Mixture Models in R

Summary

  • When we know the probabilities $\rightarrow$ estimate means and proportions
  • When we know the means and proportions $\rightarrow$ estimate the probabilities

Mixture Models in R

Let's practice!

Mixture Models in R

Preparing Video For Download...