Bernoulli Mixture Models

Mixture Models in R

Victor Medina

Researcher at The University of Edinburgh

The handwritten digits dataset

Mixture Models in R

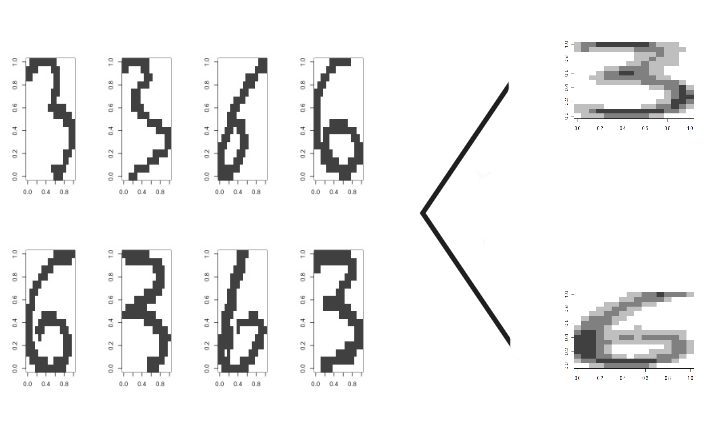
Continuous versus discrete variables

Gaussian distribution

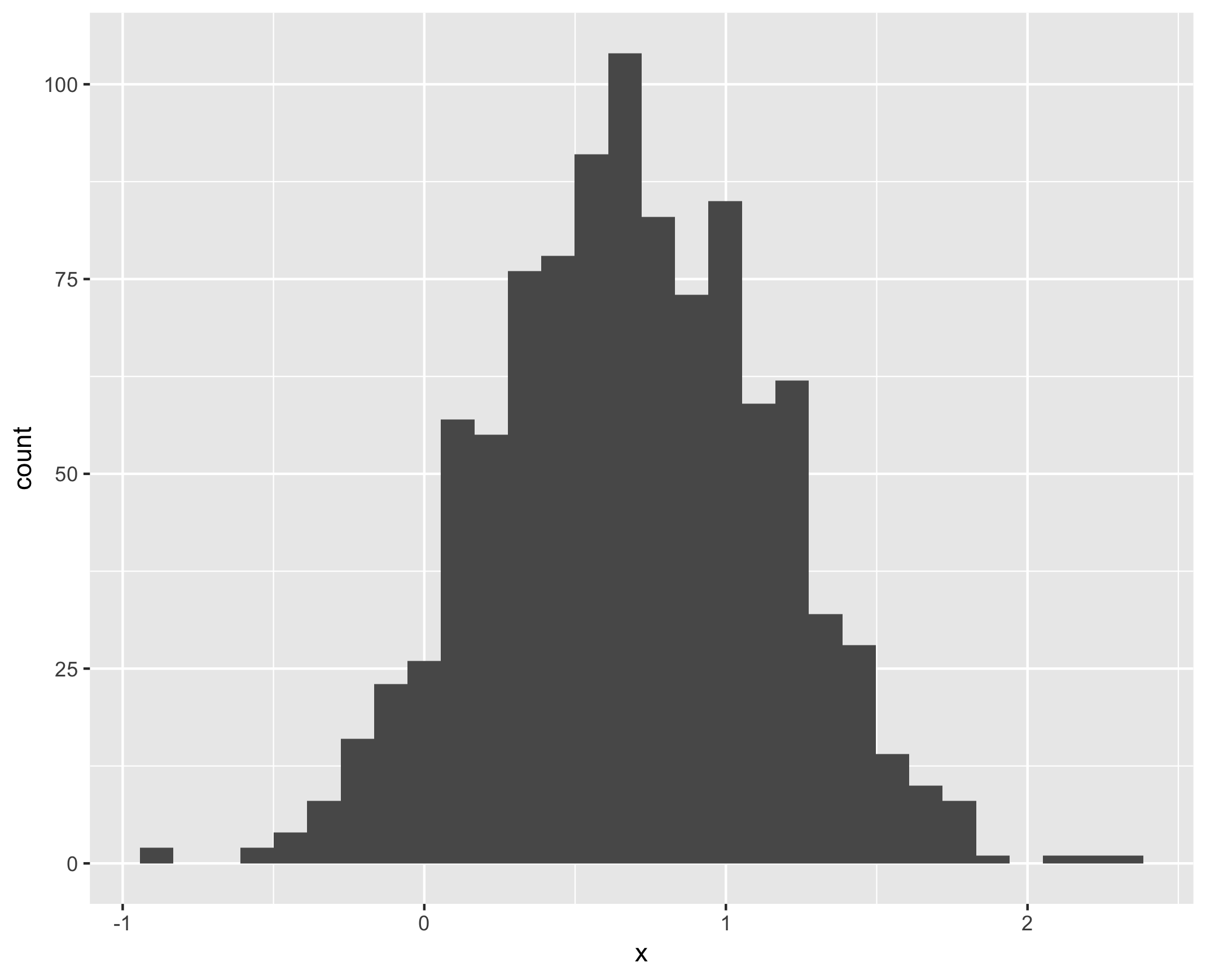
Bernoulli distribution (flipping a coin)

Mixture Models in R

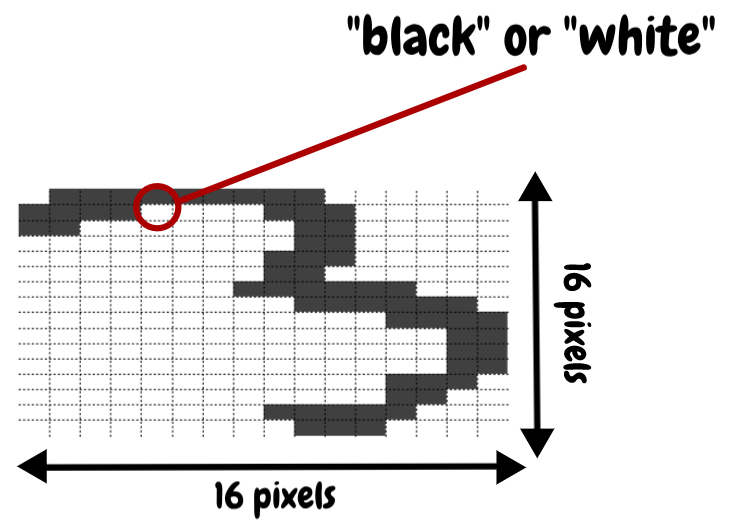
Bernoulli distribution

  • Two possible outcomes
    • "tails" or "heads"
    • "black" or "white"
  • Represented by a probability of "success" $\rightarrow p$
    • $(1- p)$ = probability for the other option
Mixture Models in R

Sample of Bernoulli distribution

p <- 0.7
bernoulli <- sample(c(0, 1), 100, replace = TRUE, prob = c(1-p, p))
head(bernoulli)

1 1 1 0 0 1
Mixture Models in R

Binary image as Bernoulli distributions

Mixture Models in R

Binary image as Bernoulli vector

Mixture Models in R
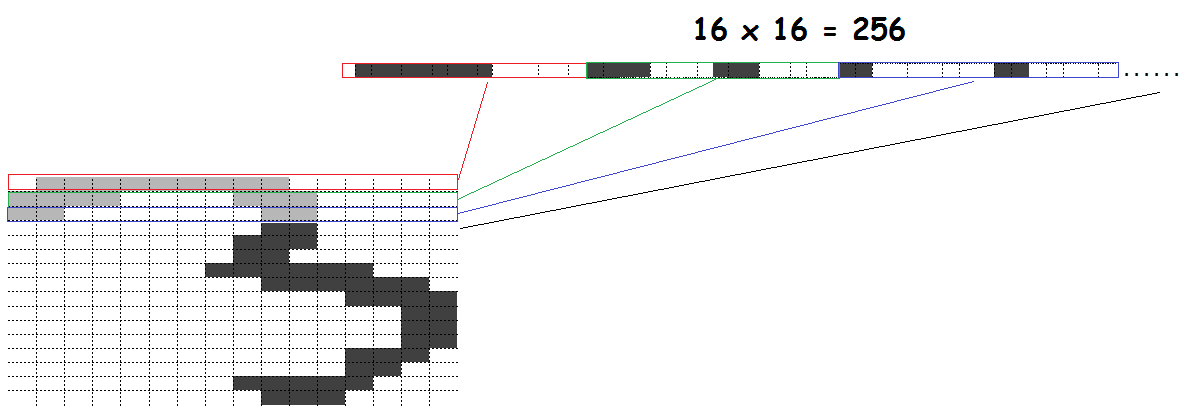
p1 <- 0.7; p2 <- 0.5; p3 <- 0.4

bernoulli_1 <- sample(c(0, 1), 100, replace = TRUE, prob = c(1-p1, p1))
bernoulli_2 <- sample(c(0, 1), 100, replace = TRUE, prob = c(1-p2, p2))
bernoulli_3 <- sample(c(0, 1), 100, replace = TRUE, prob = c(1-p3, p3))

multi_bernoulli <- cbind(bernoulli_1, bernoulli_2, bernoulli_3)

head(multi_bernoulli, 4)

     bernoulli_1 bernoulli_2 bernoulli_3
[1,]           1           0           0
[2,]           0           0           0
[3,]           0           0           1
[4,]           1           0           0

p_vector <- c(p1, p2, p3)
Mixture Models in R

Bernoulli mixture models

Handwritten digits dataset:

  1. Which is the suitable probability distribution?
    • (multivariate) Bernoulli distribution.
  2. How many subpopulations should we consider?
    • Let's try with two. That is two binary vectors of size 256.
  3. Which are the parameters and their estimations?
    • Each $p$ for each binary vector. Also the two proportions.
Mixture Models in R

Let's practice

Mixture Models in R

Preparing Video For Download...