Univariate Gaussian Mixture Models with flexmix

Mixture Models in R

Victor Medina

Researcher at The University of Edinburgh

gender %>% 
  ggplot(aes(x = Weight)) + geom_histogram(bins = 100)

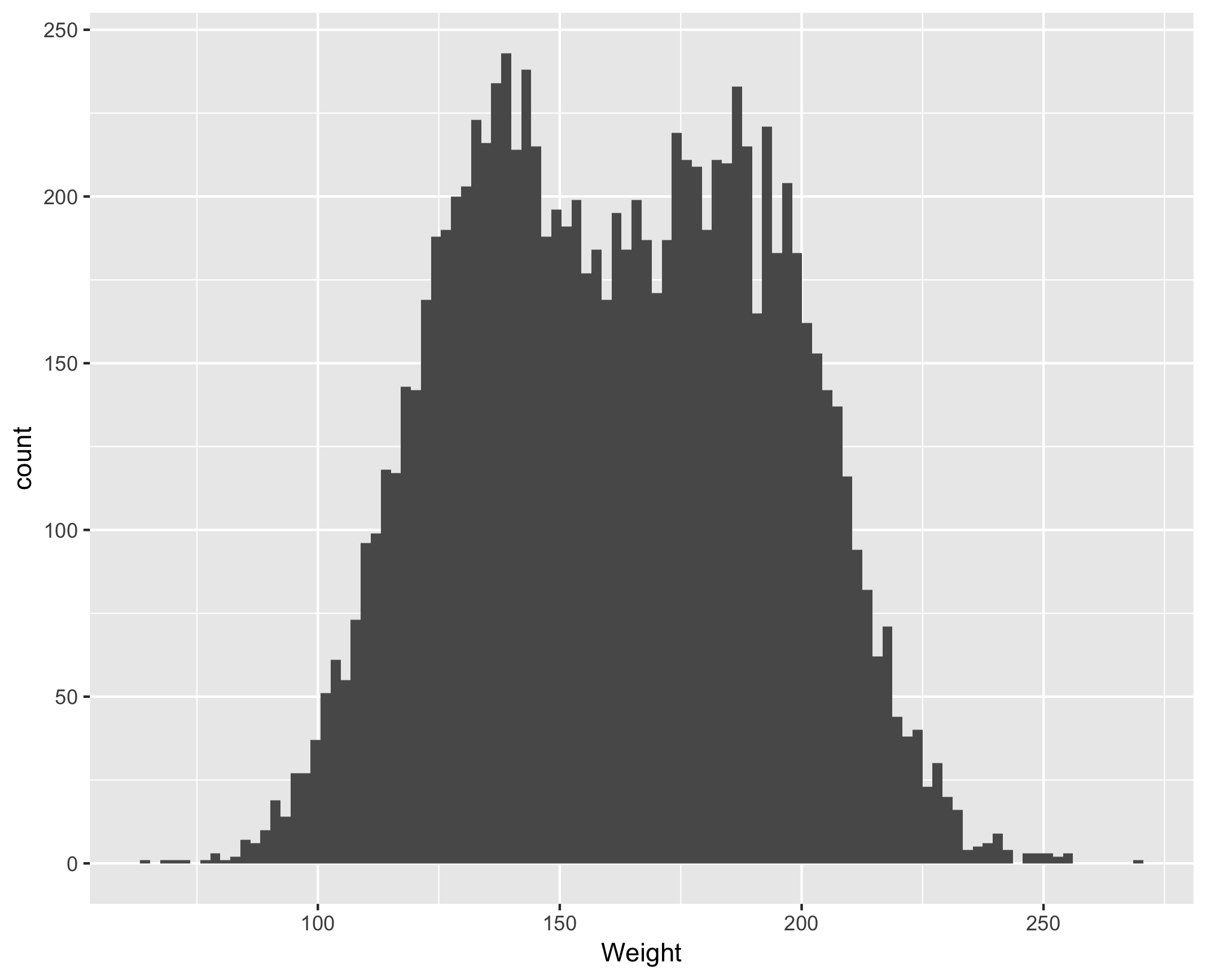
Modeling with mixture models

Which is the suitable probability distribution?
- Univariate Gaussian distributions
How many sub-populations should we consider?
- 2 clusters
Which are the parameters and their estimations?
- EM algorithm implemented in flexmix to estimate the means, the standard deviations and the proportions

flexmix function

flexmix(formula, data, k, model, control, ...)

formula: description of the model to be fit ($variable \sim 1$)
data: data frame
k: number of clusters
model: specifies the distribution (FLXMCnorm1, FLXMCmvnorm, FLXMCmvbinary, FLXMRglm, FLXMCmvpois)
control: specifies the max number of iterations, the tolerance, etc.

fit_mixture <- flexmix(Weight ~ 1, # the means and sds are constant
                data = gender, # the data frame
                k = 2, # the number of clusters,
                model = FLXMCnorm1(), # univariate Gaussian    
                control = list(tol = 1e-15, # tolerance for EM stop
                               verbose = 1, # show partial results
                               iter = 1e4)) # max number of iterations

Classification: weighted 
   1 Log-likelihood :  -48880.0782 
   2 Log-likelihood :  -48880.0745 
   3 Log-likelihood :  -48880.0732 
   4 Log-likelihood :  -48880.0727
   .    .   .   .   .   .   .   .
3454 Log-likelihood :  -48518.3717 
3455 Log-likelihood :  -48518.3717 
3456 Log-likelihood :  -48518.3717 
3457 Log-likelihood :  -48518.3717 
converged

The proportions: prior function

proportions <- prior(fit_mixture)
proportions

0.4929668 0.5070332

Both distributions

parameters(fit_mixture)

                    Comp.1    Comp.2
coef.(Intercept) 135.54652 186.61583
sigma             18.94726  19.96097

Each of them

comp_1 <- parameters(fit_mixture, component = 1)
comp_2 <- parameters(fit_mixture, component = 2)
comp_2

                    Comp.2
coef.(Intercept) 186.61583
sigma             19.96097

Visualize the resulting distributions

gender %>%
   ggplot() + geom_histogram(aes(x = Weight, y = ..density..)) + 
   stat_function(geom = "line", fun = fun_prop, 
                 args = list(mean = comp_1[1], 
                             sd = comp_1[2], 
                             proportion = proportions[1])) +
   stat_function(geom = "line", fun = fun_prop, 
                 args = list(mean = comp_2[1], 
                             sd = comp_2[2], 
                             proportion = proportions[2]))

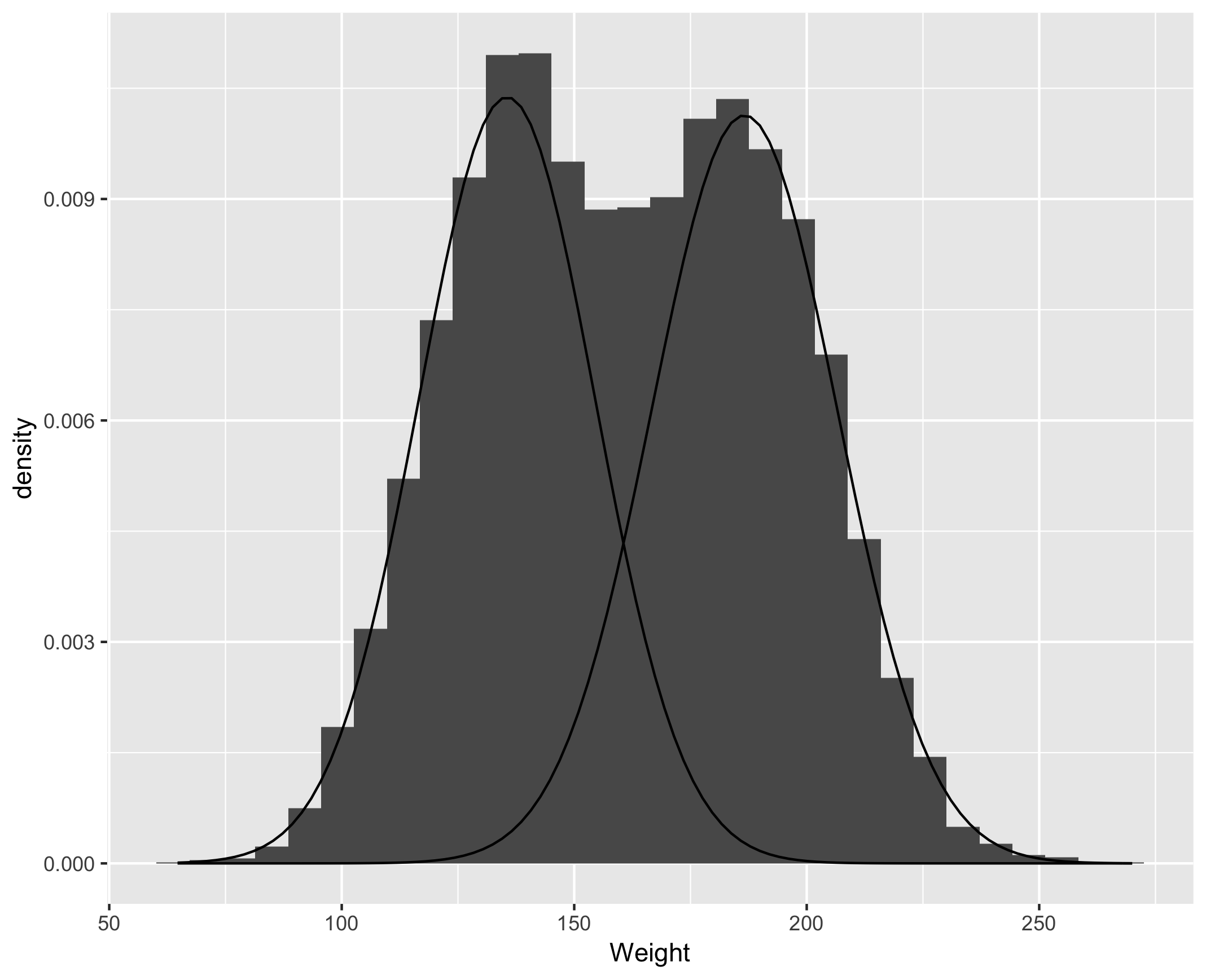
posterior function

posterior(fit_mixture) %>% head()

             [,1]      [,2]
[1,] 6.836341e-06 0.9999932
[2,] 4.421760e-01 0.5578240
[3,] 5.994160e-04 0.9994006
[4,] 1.998798e-04 0.9998001
[5,] 1.547774e-03 0.9984522
[6,] 7.544450e-01 0.2455550

clusters function

clusters(fit_mixture) %>% head()

2 2 2 2 2 1

Assignments comparison

table(gender$Gender, clusters(fit_mixture))

            1    2
  Female 4500  500
  Male    444 4556

Let's practice!

Mixture Models in R