The kernel trick

Support Vector Machines in R

Kailash Awati

Instructor

The basic idea

  • Devise a transformation that makes the problem linearly separable.
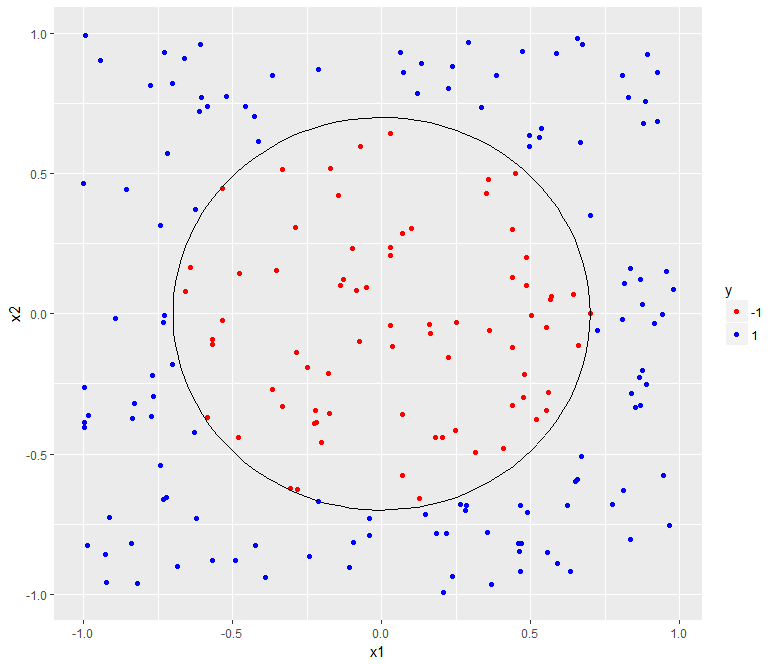
  • We'll see how to do this for a radially separable dataset.
Support Vector Machines in R

Chapter 3.3 - radially separable dataset with decision boundary

Support Vector Machines in R

Transforming the problem

  • Equation of boundary is $x_1 ^ 2 + x_2 ^ 2 = 0.49$
  • Map $x_1 ^ 2$ to a new variable $X_1$ and $x_2 ^ 2$ to $X_2$
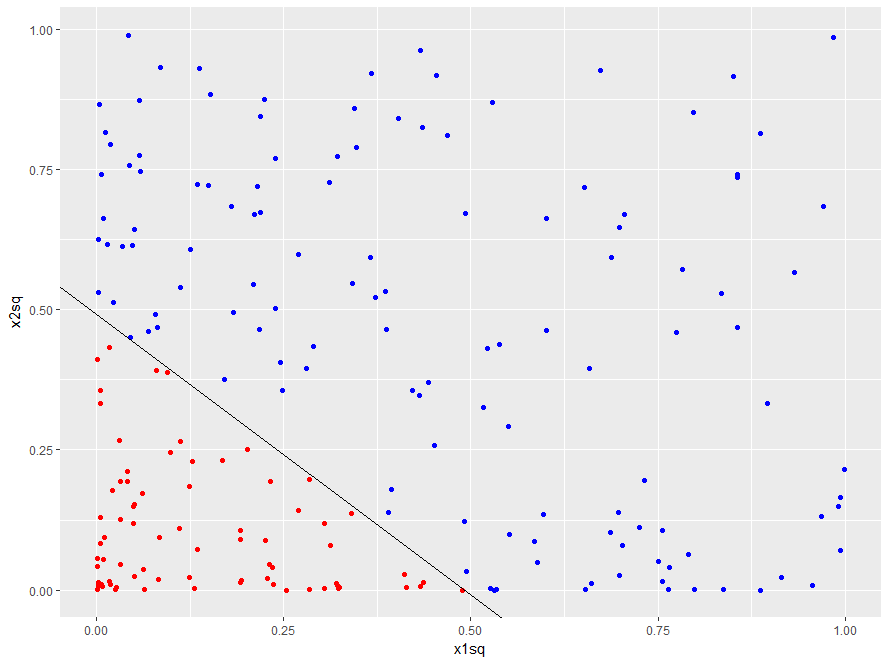
  • The equation of boundary in the $X_1 - X_2$ space becomes...
  • $X_1 + X_2 = 0.49$ (a line!!)
Support Vector Machines in R

Plot in X1-X2 space - code

  • Use ggplot() to plot the dataset in $X_1 - X_2$ space
  • Equation of boundary $X_2 = -X_1 + 0.49$:
    • $slope = -1$
    • $yintercept = 0.49$
p <- ggplot(data = df4, aes(x = x1sq, y = x2sq, color = y)) + 
  geom_point() + 
  scale_color_manual(values = c("red", "blue")) +
  geom_abline(slope = -1, intercept = 0.49)

p
Support Vector Machines in R

Chapter 3.3 - transformed radially separable dataset with decision boundary

Support Vector Machines in R

The Polynomial Kernel - Part 1

  • Polynomial kernel: (gamma * (u.v) + coef0) ^ degree
    • degree is the degree of the polynomial
    • gamma and coef0 are tuning parameters
    • u, v are vectors (datapoints) belonging to the dataset
  • We can guess we need a 2nd degree polynomial (transformation)
Support Vector Machines in R

Kernel functions

  • The math formulation of SVMs requires transformations with specific properties.
  • Functions satisfying these properties are called kernel functions
  • Kernel functions are generalizations of vector dot products
  • Basic idea - use a kernel that separates the data well!
Support Vector Machines in R

Radially separable dataset - quadratic kernel

  • 80/20 train/test split
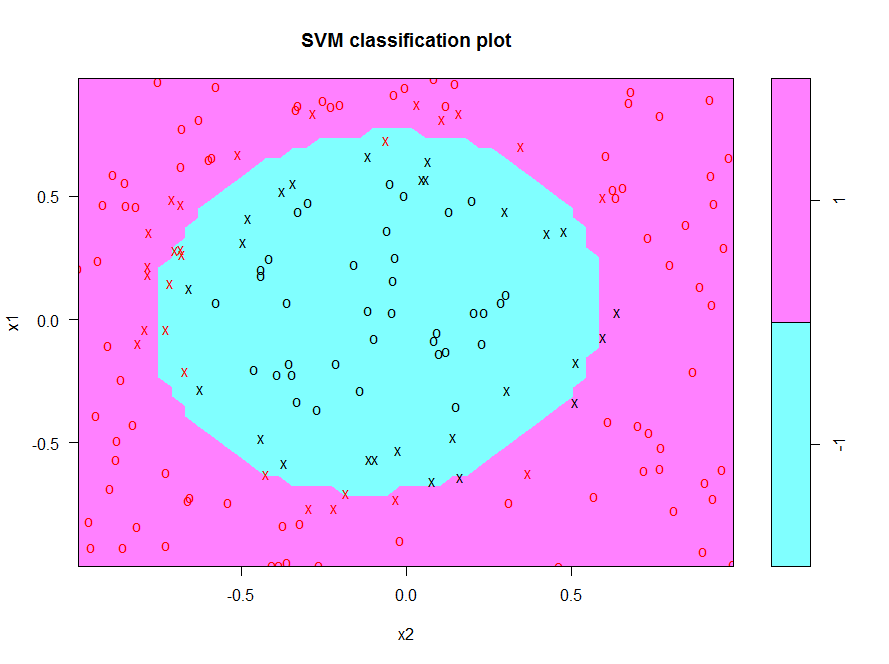
  • Build a quadratic SVM for the radially separable dataset:
    • Set degree = 2
    • Set default values of cost, gamma and coef0 (1, 1/2 and 0)
svm_model <- svm(y ~ ., data = trainset, type = "C-classification", kernel = "polynomial", degree = 2)
# Predictions
pred_test <- predict(svm_model, testset)
mean(pred_test == testset$y)

0.9354839

# Visualize model
plot(svm_model, trainset)
Support Vector Machines in R

Chapter 3.3 - radially separable dataset, default cost quadratic kernel, plot using svm.plot

Support Vector Machines in R

Time to practice!

Support Vector Machines in R

Preparing Video For Download...