More Probability Concepts
Statistical Simulation in Python

Tushar Shanker
Data Scientist
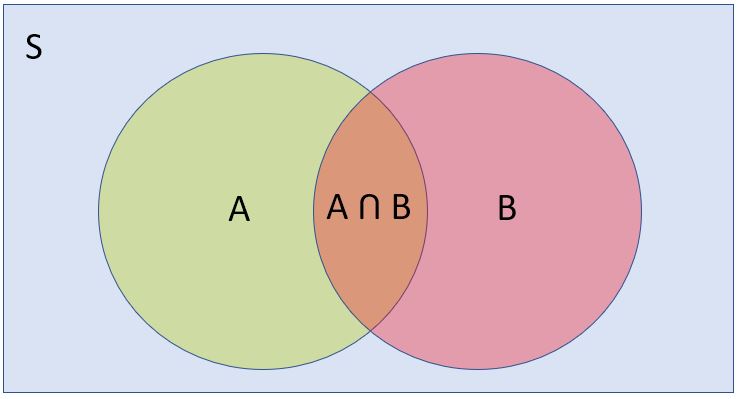
Conditional Probability
- Conditional Probability
- $P(A|B) = \dfrac{P(A \cap B)}{P(B)}$
Conditional Probability
Conditional Probability
$P(A|B) = \dfrac{P(A \cap B)}{P(B)}$
$P(B|A) = \dfrac{P(B \cap A)}{P(A)}$
$P(A \cap B) = P(B \cap A)$
Bayes Rule
Conditional Probability
$P(A|B) = \dfrac{P(A \cap B)}{P(B)}$
Bayes' rule: $P(A|B) = \dfrac{P(B|A) P(A) }{P(B)}$
Independent Events
Independent Events
$P(A \cap B) = P(A)P(B)$
Conditional Probability: $P(A|B) = \dfrac{P(A \cap B)}{P(B)} = \dfrac{P(A)P(B)}{P(B)} = P(A)$
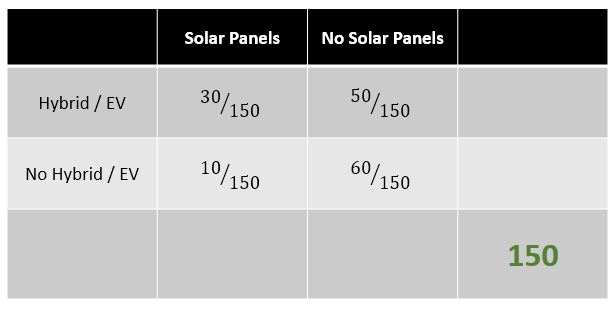
Solar Panels & Clean Vehicles
- Number of houses = 150
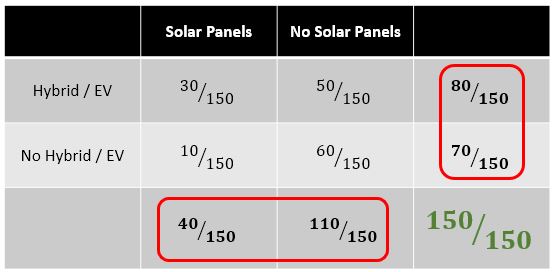
Solar Panels & Clean Vehicles
$P(\text{Solar}) = P(\text{Solar} \cap \text{Hybrid, EV}) + P(\text{Solar} \cap \text{No Hybrid, EV}) = \frac{30}{150} + \frac{10}{150}=\frac{40}{150}$
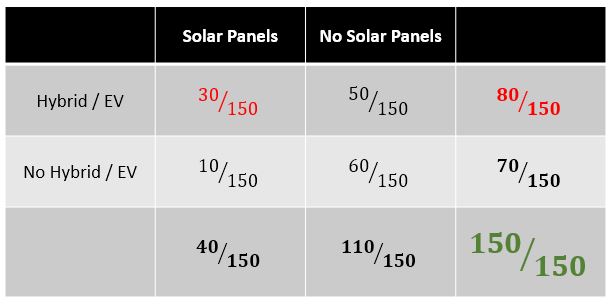
Solar Panels & Clean Vehicles
$P(\text{Solar} | \text{Hybrid, EV}) = \dfrac{P(\text{Solar} \cap \text{Hybrid, EV})}{P(\text{Hybrid, EV})} = \frac{30}{80} = 0.375$
Let's practice!
Statistical Simulation in Python