Monte Carlo integration
Statistical Simulation in Python

Tushar Shanker
Data Scientist
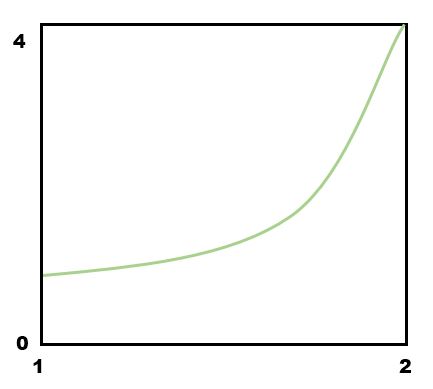
Definite integration
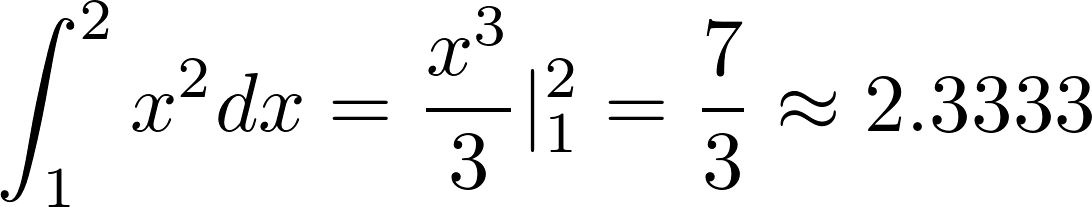
Monte Carlo integration
- Calculate overall area.
- Randomly sample points in the area.
- Multiply the fraction of the points below the curve by overall area.
- $f(x) = x^2$
Monte Carlo integration
- Calculate overall area.
- Randomly sample points in the area.
- Multiply the fraction of the points below the curve by overall area.
Calculate Overall Area
- $\int_{1}^{2}x^{2}dx$
- $x_{min} = 1, x_{max} = 2$
- $\min(0, f_{min}(x)) = 0, f_{max}(x) = 4$
- $\text{Overall Area} = 4$
Monte Carlo integration
- Calculate overall area.
- Randomly sample points in the area.
- Multiply the fraction of the points below the curve by overall area.
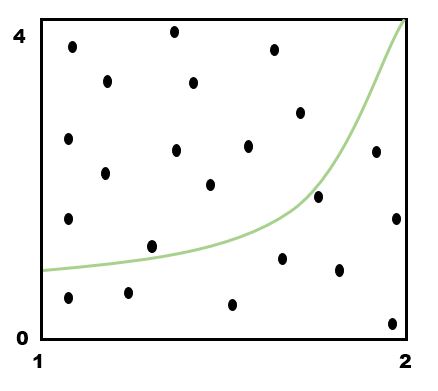
Random Sampling
Monte Carlo integration
- Calculate overall area.
- Randomly sample points in the area.
- Multiply the fraction of the points below the curve by overall area.
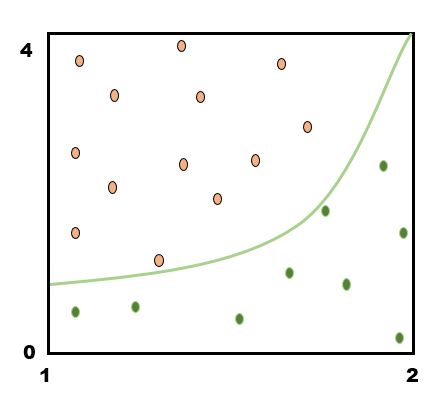
Fraction of Area
- $\text{Overall Area} \times \text{fraction} = 2.303$
- $\text{Actual Answer} = 2.333$
Let's practice!
Statistical Simulation in Python