Kaplan-Meier estimate
Survival Analysis in R

Heidi Seibold
Statistician at LMU Munich
Survival function
Theory
$S(t) = 1 - F(t) = P(T > t)$
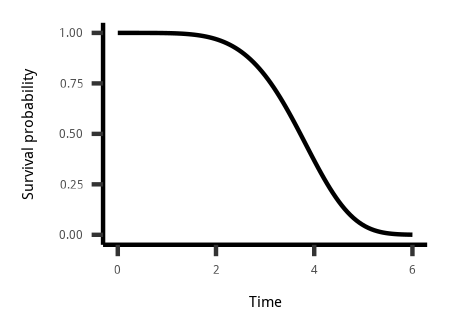
Estimation
$\hat{S}(t) = \prod\limits_{i: ~ t_i \leq t} \frac{n_i-d_i}{n_i}$
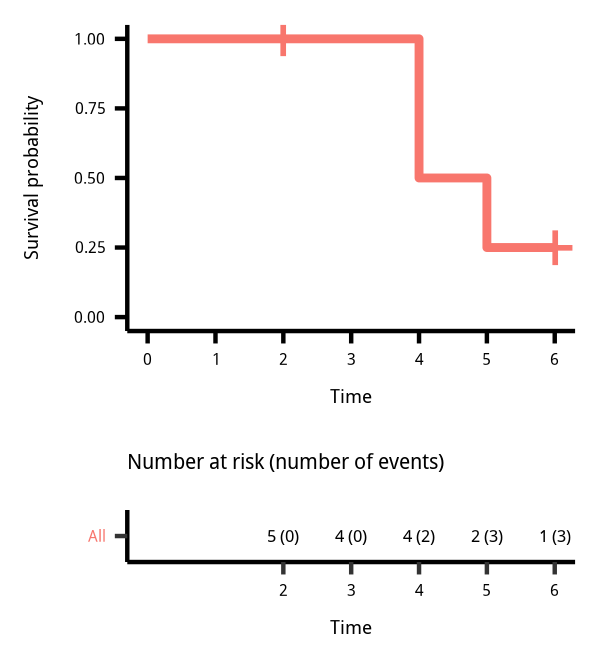
Survival function estimation
Data
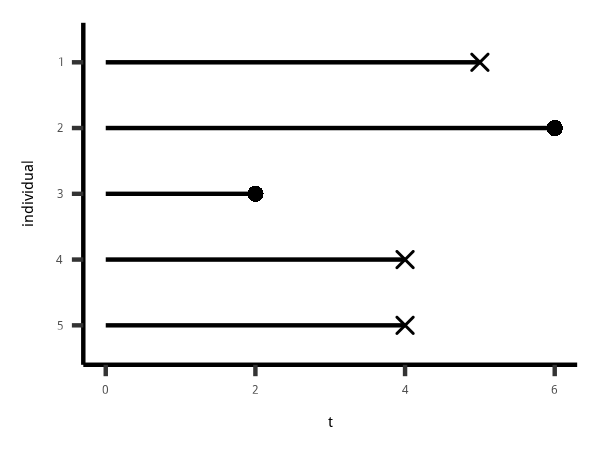
Estimation
$\hat{S}(t) = \prod\limits_{i: ~ t_i \leq t} \frac{n_i-d_i}{n_i}$

Survival function estimation: Kaplan-Meier estimate
$\hat{S}(t) = \prod\limits_{i: ~ t_i \leq t} \frac{n_i-d_i}{n_i}$
$\hat{S}(2) = \frac{5 - 0}{5} = \frac{5}{5} = 1$
$\hat{S}(3) = \frac{4 - 0}{4} = \frac{4}{4} = 1$
$\hat{S}(4) = \frac{4 - 2}{4} = \frac{2}{4} = \frac{1}{2} = 0.5$
$\hat{S}(5) = \frac{1}{2} \cdot \frac{2 - 1}{2} = \frac{1}{4} = 0.25$
$\hat{S}(6) = \frac{1}{4} \cdot \frac{1 - 0}{1} = \frac{1}{4} = 0.25$

Survival function estimation: Kaplan-Meier estimate
km <- survfit(Surv(time, event) ~ 1)ggsurvplot(km, conf.int = FALSE, risk.table = "nrisk_cumevents", legend = "none")
Let's practice!
Survival Analysis in R

