Improve the fit of your models

Machine Learning in the Tidyverse

Dmitriy (Dima) Gorenshteyn

Lead Data Scientist, Memorial Sloan Kettering Cancer Center

Multiple Linear Regression model

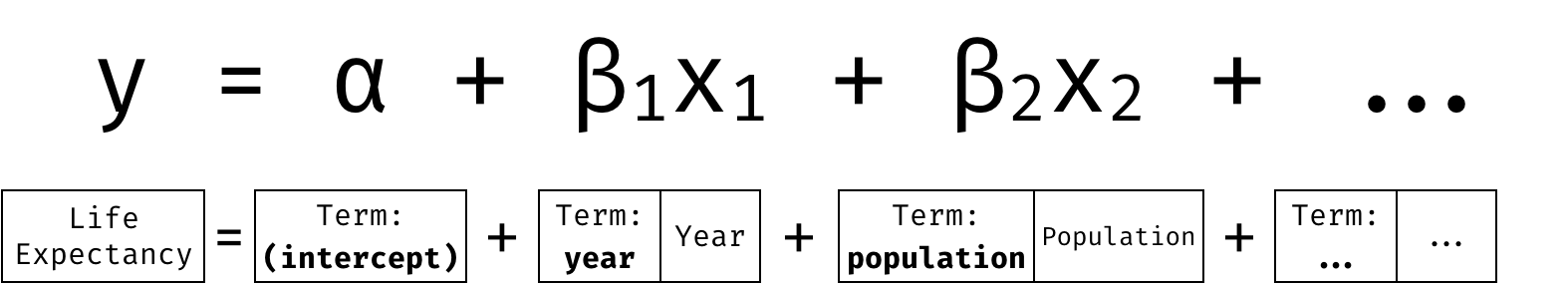
Available Features: year, population, infant_mortality, fertility, gdpPercap

Using all features

Simple Linear Model: life_expectancy ~ year

gap_models <- gap_nested %>%
 mutate(model = map(data, ~lm(formula = life_expectancy ~ year, data = .x)))

Multiple Linear Model: life_expectancy ~ year + population + ...

Multiple Linear Model: life_expectancy ~ .

gap_fullmodels <- gap_nested %>%
 mutate(model = map(data, ~lm(formula = life_expectancy ~ ., data = .x)))

tidy(gap_fullmodels$model[[1]])

              term      estimate    std.error  statistic      p.value
1      (Intercept) -1.830195e+03 1.502271e+02 -12.182848 5.325478e-16
2             year  9.814091e-01 7.800580e-02  12.581232 1.693870e-16
3 infant_mortality -1.603504e-01 4.021732e-03 -39.870986 2.525847e-37
4        fertility -2.600935e-01 1.648652e-01  -1.577614 1.215074e-01

augment(gap_fullmodels$model[[1]])

   life_expectancy year infant_mortality fertility population ...   .fitted
1            47.50 1960            148.2      7.65   11124892 ...  47.45394 
2            48.02 1961            148.1      7.65   11404859 ...  48.35078 
3            48.55 1962            148.2      7.65   11690152 ...  49.26449

glance(gap_fullmodels$model[[1]])

  r.squared adj.r.squared     sigma statistic      p.value df    logLik ...
1 0.9990732     0.9989724 0.3160595  9917.133 1.562325e-68  6 -10.70225 ...

Adjusted $R^2$

glance(gap_fullmodels$model[[1]])

  r.squared adj.r.squared     sigma statistic      p.value df    logLik ...
1 0.9990732     0.9989724 0.3160595  9917.133 1.562325e-68  6 -10.70225 ...

Let's practice!

Machine Learning in the Tidyverse