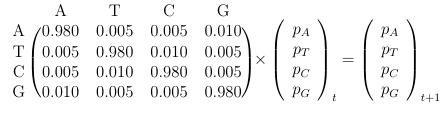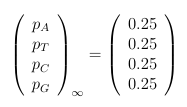Some More on Eigenvalues and Eigenvectors

Linear Algebra for Data Science in R

Eric Eager

Data Scientist at Pro Football Focus

What's Going On?

If the eigenvalues $\lambda_1, \lambda_2, ..., \lambda_n$ of $A$ are distinct and $\vec{v}_1, \vec{v}_2, ..., \vec{v}_n$ is a set of associated eigenvectors, then this set of vectors forms a basis for the set of $n$-dimensional vectors.
In other words, if we assume that the matrix $A$ has a basis of eigenvectors $\vec{v}_1, \vec{v}_2, ... \vec{v}_n$, with associated, distinct eigenvalues $\lambda_1, \lambda_2, ... \lambda_n$, then every $n$-dimensional vector can be expressed as a linear combination of these vectors, i.e. $$\vec{x} = c_1\vec{v}_1 + c_2\vec{v}_2 + ... + c_n\vec{v}_n.$$

What's Going On?

Applying the matrix $A$ to $\vec{x}$, and using the fact that $A\vec{v}_j = \lambda_j \vec{v}_j,$ notice the following simple decomposition

$$A\vec{x} = c_1\lambda_1\vec{v}_1 + c_2\lambda_2\vec{v}_2 + ... + c_n\lambda_n\vec{v}_n.$$

Hence, eigenpairs turn matrix multiplication into a linear combination of scalar multiplications!

Iterating the Matrix

If we iteratively multiply by the matrix $A$:

$$A A\vec{x} = $$ $$ = A(c_1\lambda_1\vec{v}_1 + c_2\lambda_2\vec{v}_2 + ... + c_n\lambda_n\vec{v}_n)$$ $$ = c_1\lambda_1^2\vec{v}_1 + c_2\lambda_2^2\vec{v}_2 + ... + c_n\lambda_n^2\vec{v}_n,$$

or, in general: $$A^t\vec{x} = c_1\lambda_1^t\vec{v}_1 + c_2\lambda_2^t\vec{v}_2 + ... + c_n\lambda_n^t\vec{v}_n.$$

Thus, successive matrix multiplication is not successive scalar multiplication (exponentiation)!

Also, if one of the eigenvalues is larger than all of the others, these differences will be exacerbated as $t$ grows.

Example with Allele Frequencies

print(M)

eigen(M)

      [,1]  [,2]  [,3]  [,4]
[1,] 0.980 0.005 0.005 0.010
[2,] 0.005 0.980 0.010 0.005
[3,] 0.005 0.010 0.980 0.005
[4,] 0.010 0.005 0.005 0.980

eigen() decomposition
$`values`
[1] 1.00 0.98 0.97 0.97

$vectors
     [,1] [,2]          [,3]          [,4]
[1,] -0.5  0.5  0.000000e+00  7.071068e-01
[2,] -0.5 -0.5 -7.071068e-01  1.132427e-14
[3,] -0.5 -0.5  7.071068e-01 -2.442491e-15
[4,] -0.5  0.5 -1.382228e-14 -7.071068e-01

print(M)

      [,1]  [,2]  [,3]  [,4]
[1,] 0.980 0.005 0.005 0.010
[2,] 0.005 0.980 0.010 0.005
[3,] 0.005 0.010 0.980 0.005
[4,] 0.010 0.005 0.005 0.980

Lambda <- eigen(M)
v1 <- Lambda$vectors[, 1]/sum(Lambda$vectors[, 1])
print(v1)

0.25 0.25 0.25 0.25

Let's practice

Linear Algebra for Data Science in R