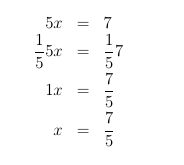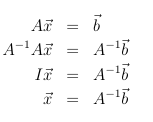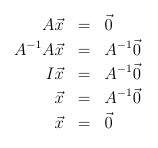Solving Matrix-Vector Equations

Linear Algebra for Data Science in R

Eric Eager

Data Scientist at Pro Football Focus

print(A)

     [,1] [,2]
[1,]    1   -2
[2,]    0    4

print(b)

1 -2

Solving $A\vec{x} = \vec{b}$ using $\vec{x} = A^{-1}\vec{b}$:

x <- solve(A)%*%b
print(x)

     [,1]
[1,]  0.0
[2,] -0.5

x <- solve(A)%*%b
print(x)

     [,1]
[1,]  0.0
[2,] -0.5

Checking your solution by plugging in the solution $\vec{x}$:

A%*%x

    [,1]
[1,]    1
[2,]   -2

Which is equal to the given $\vec{b}$:

print(b)

1 -2

Additional Conditions for Unique Solutions

Thus, the only solution to the homogeneous equation $A\vec{x} = \vec{0}$ is the trivial solution $\vec{x} = \vec{0}$.

print(A)

     [,1] [,2]
[1,]    1   -2
[2,]    0    4

b <- rep(0, 2)
print(b)

0 0

solve(A)%*%b

     [,1]
[1,]    0
[2,]    0

If $A$ is an $n$ by $n$ square matrix, then the following conditions are equivalent and imply a unique solution to $$A\vec{x} = \vec{b}:$$

The matrix $A$ has an inverse (is invertible)
The determinant of $A$ is nonzero
The rows and columns of $A$ form a basis for the set of all vectors with $n$ elements
The homogeneous equation $A\vec{x} = \vec{0}$ has just the trivial ($\vec{x} = 0$) solution

Linear Algebra for Data Science in R