Multiple logistic regression

Generalized Linear Models in R

Richard Erickson

Instructor

Chapter overview

Multiple logistic regression
Formulas in R
Model assumptions

Why multiple regression?

Problem: Multiple predictor variables. Which one should I include?

Solution: Include all of them using multiple regression.

Multiple predictor variables

Simple linear models or simple GLM:
- Limited to 1 Slope and 1 intercept
- $y\sim \beta_0 + \beta_1 x + \epsilon$
Multiple regression
- Multiple slopes and intercepts:
- $y\sim \beta_0 + \beta_1 x_1 + \beta_2 x + \beta_3 x_3 \ldots + \epsilon$

Too much of a good thing

Theoretical maximum number of coefficients:

Maximum number of $\beta$s = Number of observations

Over-fitting:

Using too many predictors compared to number of samples

Practical maximum number of coefficients:

Number of $\beta\times10 \approx$ Number of observations

Bus data: Two possible predictors

With bus commuter data, 2 possible predictors
- Number of days one commutes: CommuteDay
- Distance of commute: MilesOneWay
Possible to build a model with both

glm(Bus ~ CommuteDay + MilesOneWay, data = bus,  family = 'binomial')

Summary of GLM with multiple predictors

Call:
glm(formula = Bus ~ CommuteDays + MilesOneWay, family = "binomial", 
    data = bus)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.0732  -0.9035  -0.7816   1.3968   2.5066  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.707515   0.119719  -5.910 3.42e-09 ***
CommuteDays  0.066084   0.023181   2.851  0.00436 ** 
MilesOneWay -0.059571   0.003218 -18.512  < 2e-16 ***
#...

Correlation between predictors

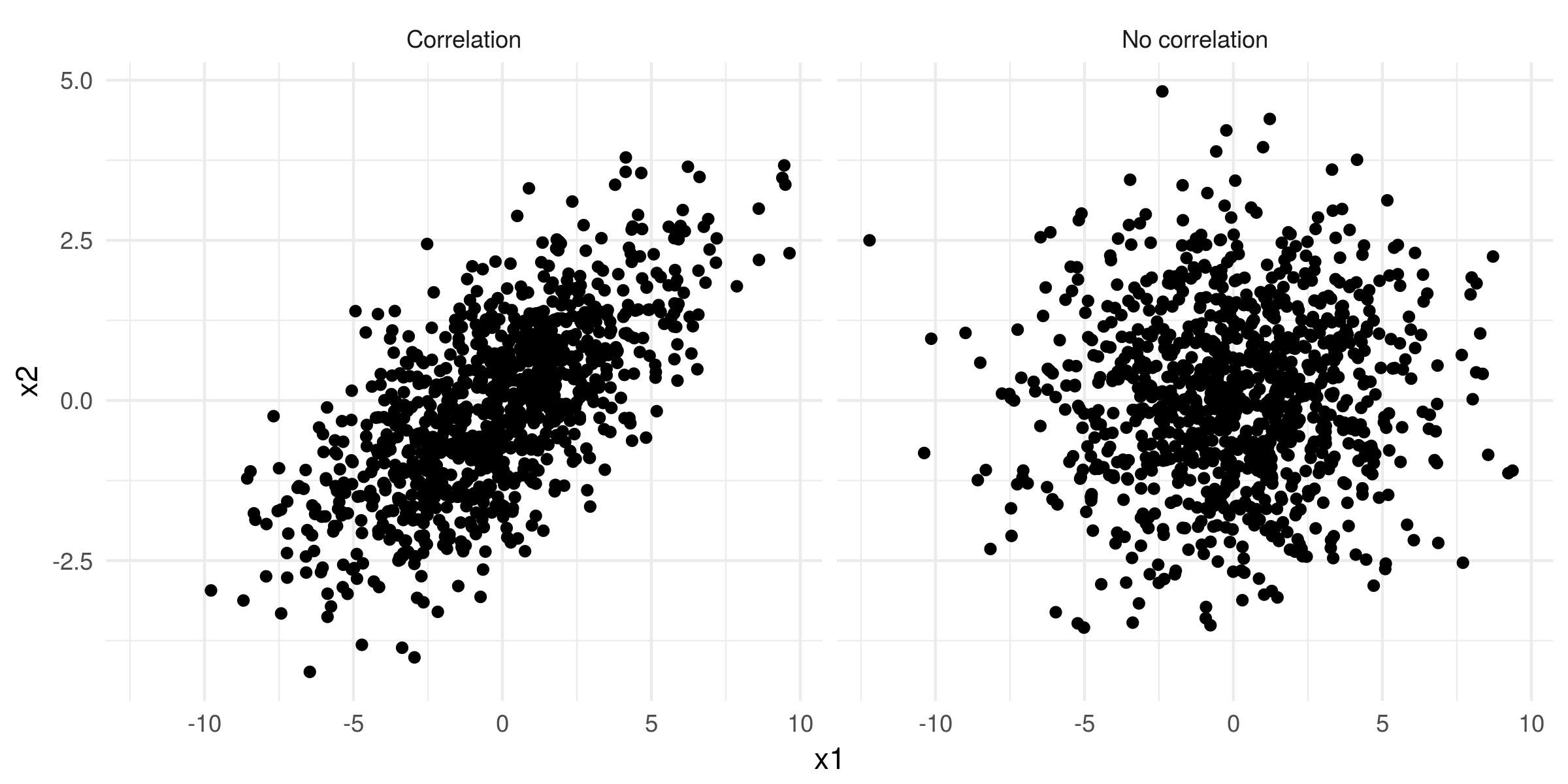
Example correlation plot

Order of coefficients

No correlation between predictors

Order not important
$y\sim x_1 + x_2 +\epsilon \approx y\sim x_2 + x_1 +\epsilon$

Correlation between predictors

Order may changes estimates
$y\sim x_1 + x_2 +\epsilon \neq y\sim x_2 + x_1 +\epsilon$

Let's practice!

Generalized Linear Models in R