Benford's Law for fraud detection
Fraud Detection in R

Bart Baesens
Professor Data Science at KU Leuven
Many datasets satisfy Benford's Law
- Data where numbers represent sizes of facts or events
- Data in which numbers have no relationship to each other
- Data sets that grow exponentially or arise from multiplicative fluctuations
- Mixtures of different data sets
- Some well-known infinite integer sequences
Preferably, more than 1000 numbers that go across multiple orders.
For example
- accounting transactions
- credit card transactions
- customer balances
- death rates
- diameter of planets
- electricity and telephone bills
- Fibonacci numbers
- incomes
- insurance claims
- lengths and flow rates of rivers
- loan data
- numbers of newspaper articles
- physical and mathematical constants
- populations of cities
- powers of 2
- purchase orders
- stock and house prices
- ...
Benford's Law for fraud detection
- Fraud is typically committed by adding invented numbers or changing real observations.
- Benford’s Law is popular tool for fraud detection and is even legally admissible as evidence in the US.
- It has for example been successfully applied for claims fraud, check fraud, electricity theft, forensic accounting and payments fraud.
- See also the book Benford's Law: Applications for forensic accounting, auditing, and fraud detection of Nigrini (John Wiley & Sons, 2012).
Be careful
Note that it is always possible that data simply does not conform to Benford's Law.
- If there is lower and/or upper bound or data is concentrated in narrow interval, e.g. hourly wage rate, height of people.
- If numbers are used as identification numbers or labels, e.g. social security number, flight numbers, car license plate numbers, phone numbers.
- Additive fluctuations instead of multiplicative fluctuations, e.g. heartbeats on a given day
Benford's Law for the first-two digits
A dataset satisfies Benford's Law for the first-two digits if the probability that the first-two digits $D_1D_2$ equal $d_1d_2$ is approximately:
$$P(D_1D_2=d_1d_2)=\log\left(1+\frac{1}{d_1d_2}\right) \qquad d_1d_2\in [10, 11, ..., 98, 99]$$
benlaw <- function(d) log10(1 + 1 / d)
benlaw(12)
0.03476211
This test is more reliable than the first digits test and is most frequently used in fraud detection.
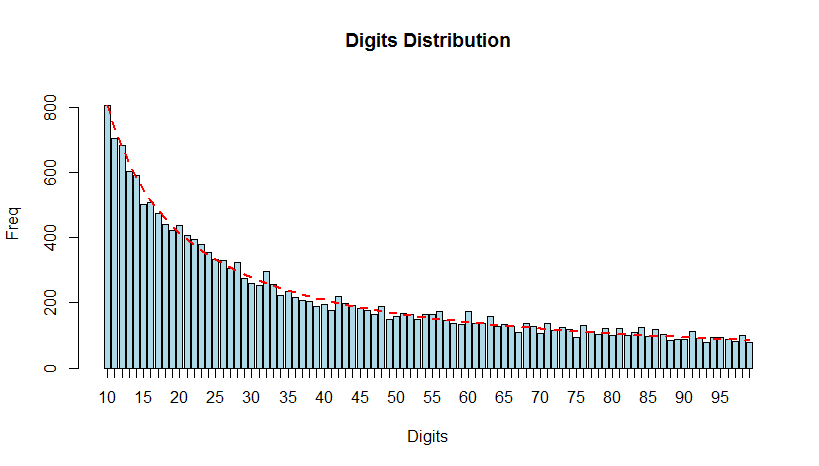
Census data
bfd.cen <- benford(census.2009$pop.2009, number.of.digits = 2)
plot(bfd.cen)
Employee reimbursements
- Internal audit department need to check employee reimbursements for fraud.
- Employees may reimburse business meals and travel expenses after mailing scanned images of receipts.
- Let us analyze the amounts that were reimbursed to employee Sebastiaan in the last 5 years.
- Dataset
expensescontains 1000 reimbursements. - We will use again the function included in package
benford.analysis.
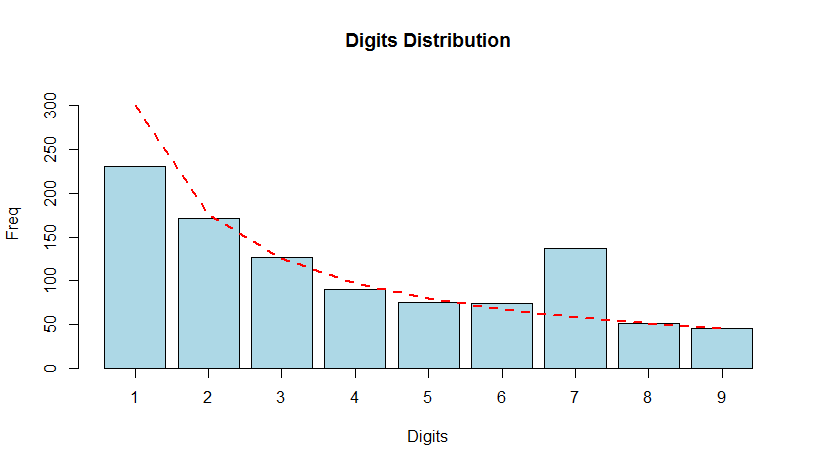
Analysis with Benford's Law for first digit
bfd1.exp <- benford(expenses, number.of.digits = 1)
plot(bfd1.exp)
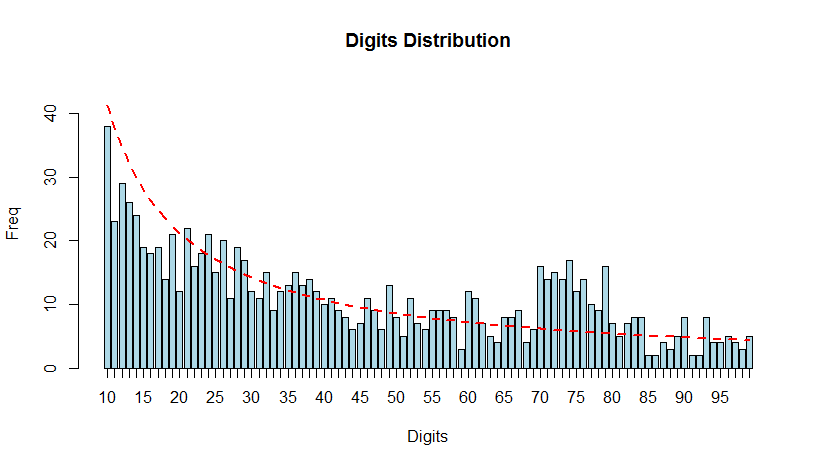
Analysis with Benford's Law for first-two digits
bfd2.exp <- benford(expenses, number.of.digits = 2)
plot(bfd2.exp)
Let's practice!
Fraud Detection in R

