Digit analysis using Benford's Law

Fraud Detection in R

Bart Baesens

Professor Data Science at KU Leuven

Introduction

Take a newspaper at a random page and write down the first or leftmost digit (1,2,...,9) of all numbers.
What are the expected frequencies of these digits?

newspaper

Introduction

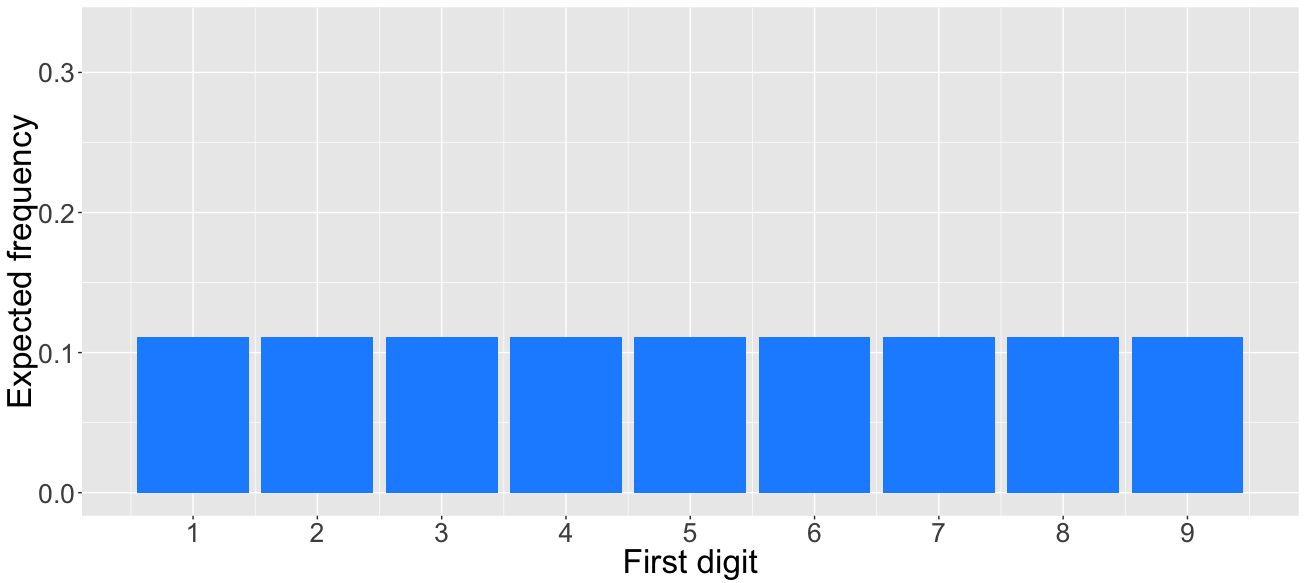
Take a newspaper at a random page and write down the first or leftmost digit (1,2,...,9) of all numbers.
What are the expected frequencies of these digits?
Natural guess will be about 1/9 = 11%

barplotrnd

Introduction

Take a newspaper at a random page and write down the first or leftmost digit (1,2,...,9) of all numbers.
What are the expected frequencies of these digits?
Natural guess will be about 1/9
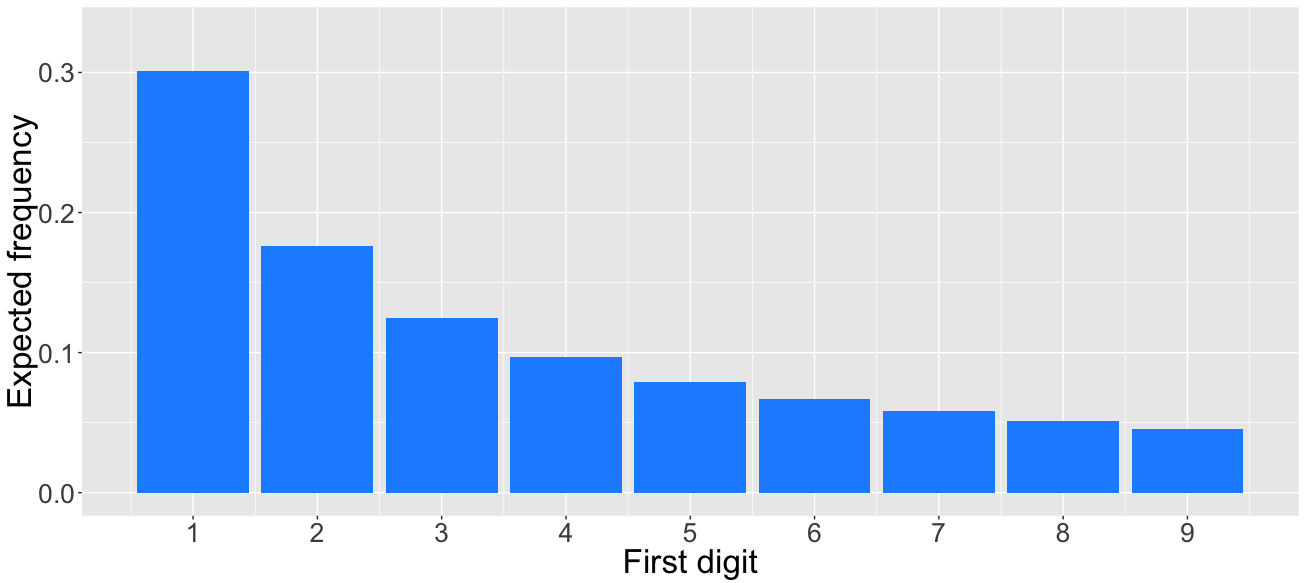
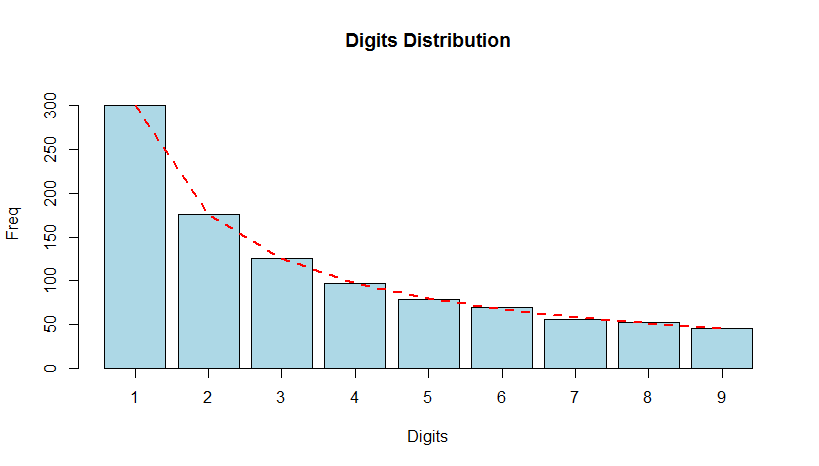
Benford's law: expected frequencies
- digit 1 $\approx$ 30%
- digit 9 $\approx$ 4.6%

barplotbf

Newcomb and Benford

"That the ten digits do not occur with equal frequency must be evident to any one making much use of logarithmic tables, and noticing how much faster the first pages wear out than the last ones." (Newcomb, 1881)
Benford observed the first digit of numbers in 20 different datasets.

newben

Benford's law for the first digit

A dataset satisfies Benford's Law for the first digit if the probability that the first digit $D_1$ equals $d_1$ is approximately: $$P(D_1=d_1)=\log(d_1+1)-\log(d_1)=\log\left(1+\frac{1}{d_1}\right) \qquad d_1=1,\ldots,9$$

Examples
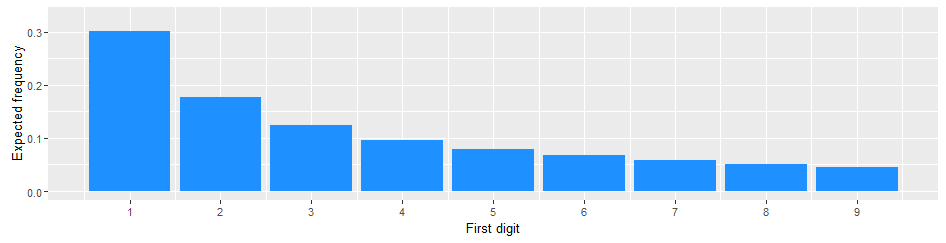
- $P(D_1=1)=\log\left(1+\frac{1}{1}\right)=\log(2)=0.3010300$
- $P(D_1=2)=\log\left(1+\frac{1}{2}\right)=\log(1.5)=0.1760913$
- $P(D_1=9)=\log\left(1+\frac{1}{9}\right)=\log(1.111111)=0.04575749$
Pinkham discovered that Benford's law is invariant by scaling.

Benford's law for the first digit

benlaw <- function(d) log10(1 + 1 / d)
benlaw(1)

0.30103

barplotbf

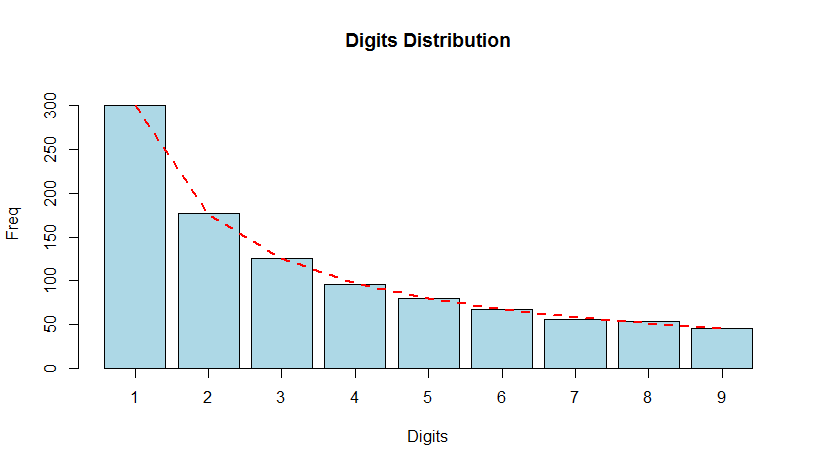
We generate the first 1000 Fibonacci numbers.

fibnum <- numeric(1000)
fibnum[1] <- fibnum[2] <- 1
for (i in 3:1000) { fibnum[i] <- fibnum[i-1] + fibnum[i-2] } 
head(fibnum)

1 1 2 3 5 8

We also generate the first 1000 powers of 2.

pow2 <- 2^(1:1000)
head(pow2)

2 4 8 16 32 64

Function `benford` from package benford.anaysis

library(benford.analysis)
bfd.fib <- benford(fibnum,
                   number.of.digits = 1)
plot(bfd.fib)

fibonacci

library(benford.analysis)
bfd.pow2 <- benford(pow2,
                    number.of.digits = 1)
plot(bfd.pow2)

pow2

Let's practice!

Fraud Detection in R