Time features

Fraud Detection in R

Bart Baesens

Professor Data Science at KU Leuven

Analyzing time

Certain events are expected to occur at similar moments in time
Example: customer making transactions at similar hours
Aim: capture information about the time aspect by meaningful features
Dealing with time can be tricky
- 00:00 = 24:00
- No natural ordering, for example 23:00 $<$ or $>$ 01:00?

Do not use arithmetic mean to compute an average timestamp!
- Example: transaction was made at 01:00, 02:00, 21:00 and 22:00
- arithmetic mean is 11:30, but no transfer was made close to that time!

head(timestamps)

"20:27:28" "21:08:41" "01:30:16" "00:57:04" "23:12:14" "22:54:16"

Convert digital timestamps to decimal format in hours

library(lubridate)
ts <- as.numeric(hms(timestamps)) / 3600

head(ts)

20.4577778 21.1447222  1.5044444  0.9511111 23.2038889 22.9044444

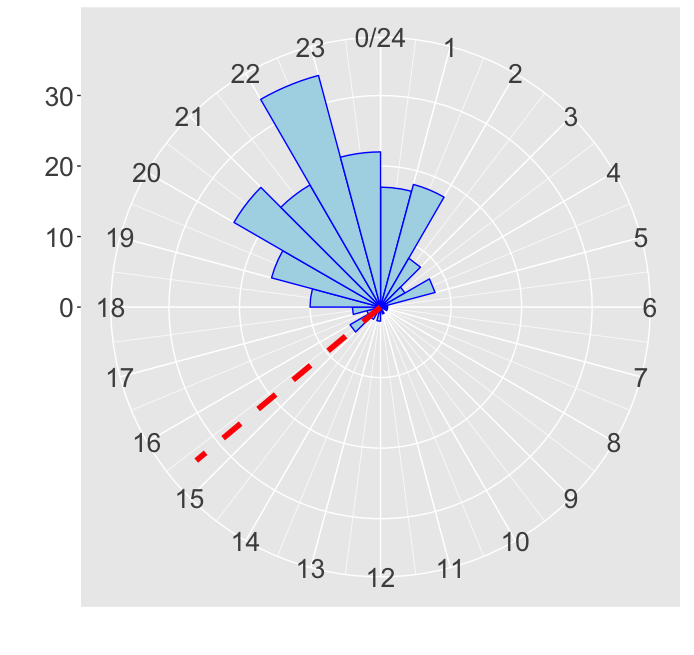
Circular histogram

library(ggplot2)

clock <- ggplot(data.frame(ts), aes(x = ts)) +
    geom_histogram(breaks = seq(0, 24), colour = "blue", fill = "lightblue") +
    coord_polar()


arithmetic_mean <- mean(ts)

clock + geom_vline(xintercept = arithmetic_mean,
                     linetype = 2, color = "red", size = 2)

Circular histogram with arithmetic mean

wrong_clock

von Mises probability distribution

Model time as a periodic variable using the von Mises distribution (Correa Bahnsen et al., 2016)
Periodic normal distribution = normal distribution wrapped around a circle
von Mises distribution of a set of timestamps $D= $ {$t_1, t_2, \ldots, t_n$}

$$D\sim vonMises\left(\mu,\kappa\right)$$

$\mu$ : periodic mean, measure of location, distribution is clustered around $\mu$
$1/\kappa$ : periodic variance; $\kappa$ is a measure of concentration

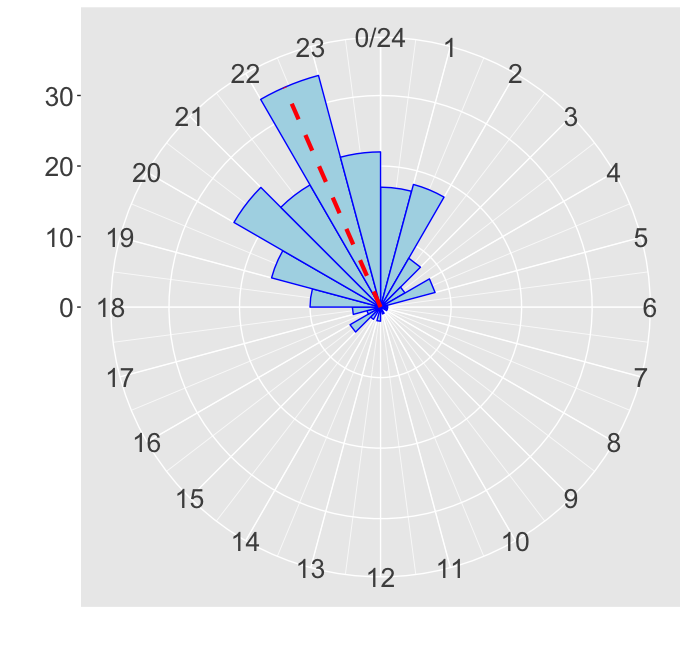
Estimate parameters $\mu$ and $\kappa$

# Convert the decimal timestamps to class "circular"
library(circular)
ts <- circular(ts, units = "hours", template = "clock24")

head(ts)

Circular Data: 
[1] 20.457889 21.144607  1.504422  0.950982 23.203917  4.904397

estimates <- mle.vonmises(ts)
p_mean <- estimates$mu %% 24
concentration <- estimates$kappa

Circular histogram with periodic mean

correct_clock

Confidence interval

Extract new features: confidence interval for the time of a transaction
$S= $ {$x_i^{time}|i=1,\ldots,n$} : set of transactions made by the same customer

(1) Estimate $\mu(S)$ and $\kappa(S)$ based on $S$ with mle.vonmises():

estimates <- mle.vonmises(ts)
p_mean <- estimates$mu %% 24
concentration <- estimates$kappa

(2) Calculate the density (= likelihood) of the timestamps with dvonmises():

densities <- dvonmises(ts, mu = p_mean, kappa = concentration)

Feature extraction

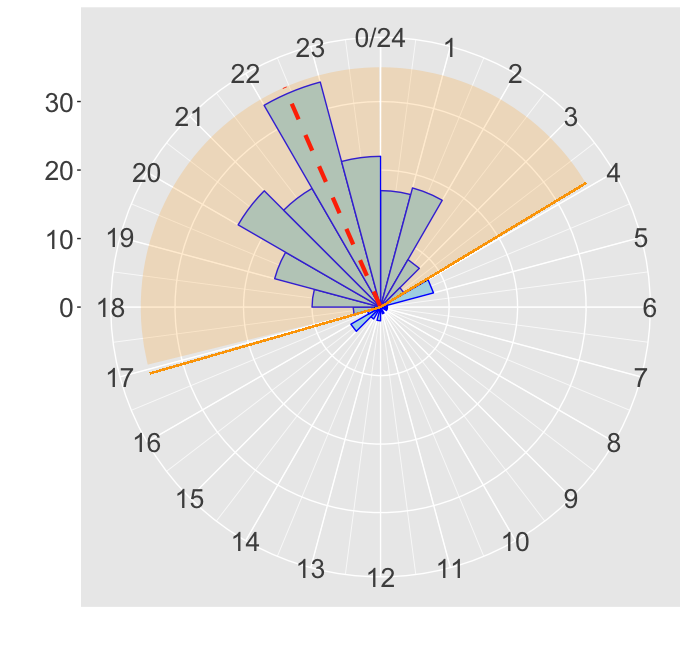
Binary feature: timestamp of a new transaction is either in the confidence interval (CI) with probability $\alpha$ (e.g. 0.90, 0.95) or not
Binary time feature is TRUE if timestamp lies inside CI and is FALSE otherwise
Timestamp is within 90% CI if its density is larger than the cutoff value:

alpha <- 0.90
quantile <- qvonmises(p = (1 - alpha)/2, 
                        mu = p_mean,
                        kappa = concentration) %% 24
cutoff <- dvonmises(quantile,
                      mu = p_mean, kappa = concentration)

time_feature <- densities >= cutoff

Confidence interval

confidence_clock

Confidence interval

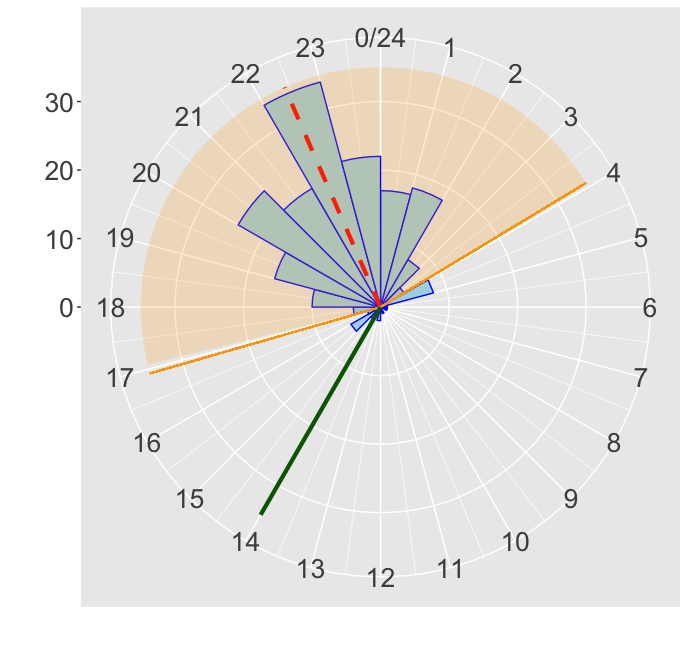
confidence_clock_2

Example

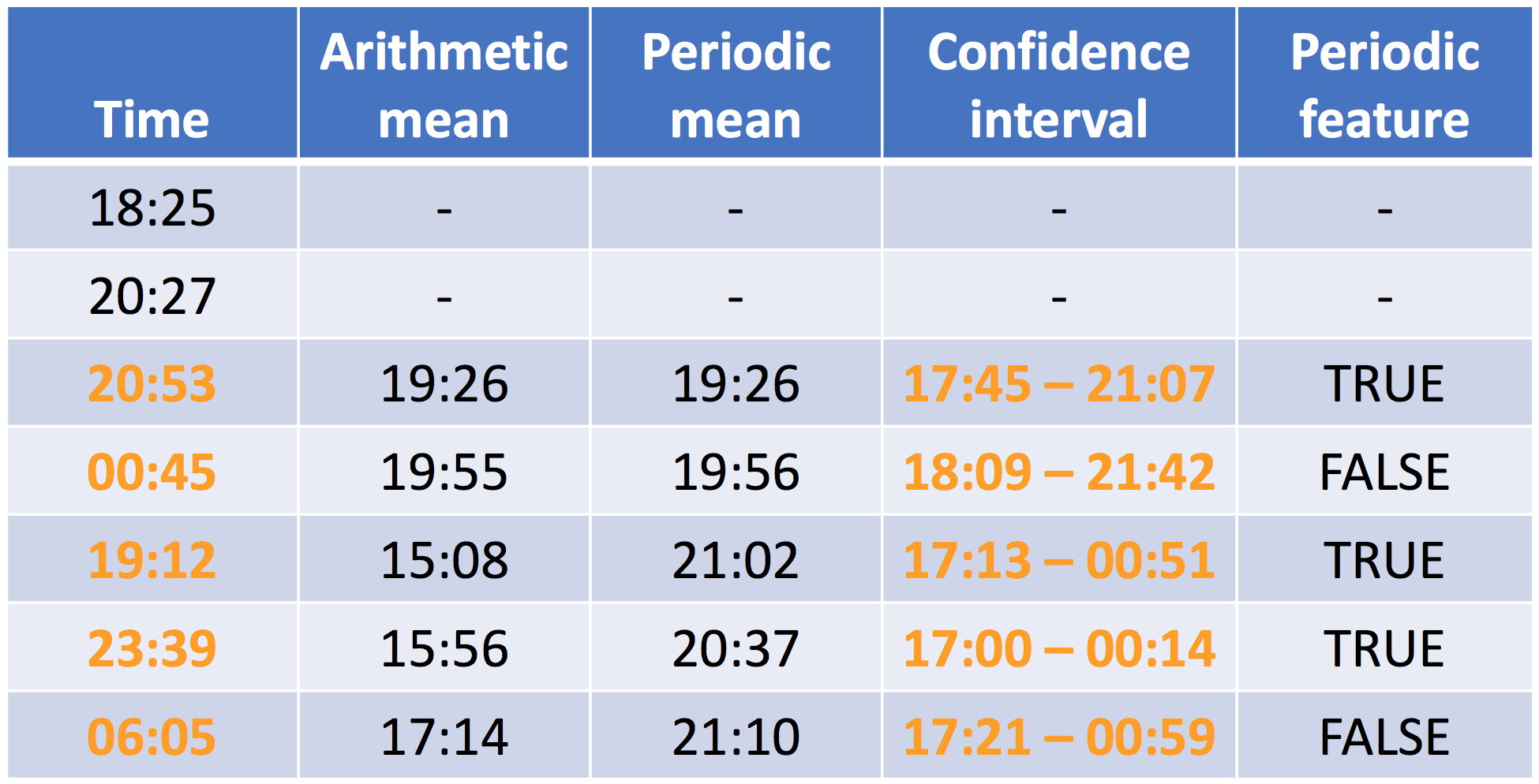
$$ $$ time_table

Confidence interval with moving time window

## ts contains the timestamps 18.42, 20.45, 20.88, 0.75, 19.20, 23.65 and 6.08

time_feature = c(NA, NA)
for (i in 3:length(ts)) {
    ts_history <- ts[1:(i-1)] ## (1) Previous timestamps

    estimates <- mle.vonmises(ts_history) ## (2) Estimate mu and kappa on historic timestamps
    p_mean <- estimates$mu %% 24
    concentration <- estimates$kappa

    dens_i <- dvonmises(ts[i], mu = p_mean, kappa = concentration) ## (3) Estimate density of current timestamp

    alpha <- 0.90 ## (4) Check if density is larger than cutoff with confidence level 90%
    quantile <- qvonmises((1-alpha)/2, mu=p_mean, kappa=concentration) %% 24
    cutoff <- dvonmises(quantile, mu = p_mean, kappa = concentration)
    time_feature[i] <- dens_i >= cutoff
}

print(time_feature)

NA    NA  TRUE FALSE  TRUE  TRUE FALSE

Let's practice!

Fraud Detection in R