GARCH models: The way forward

GARCH Models in R

Kris Boudt

Professor of finance and econometrics

Inventors of GARCH models

Robert Engle

Engle

Tim Bollerslev

Bollie

GARCH Models in R

Notation (i)

  • Input: Time series of returns

Predicted volatilities

GARCH Models in R

Notation (ii)

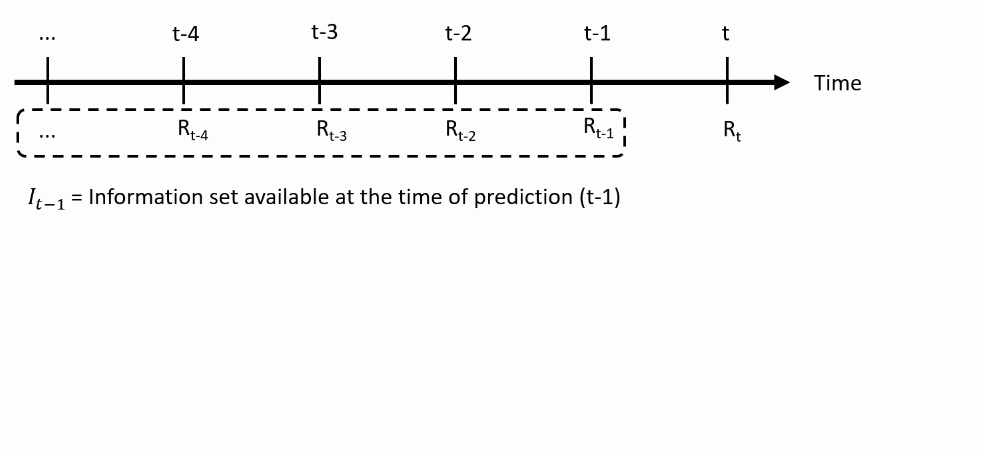
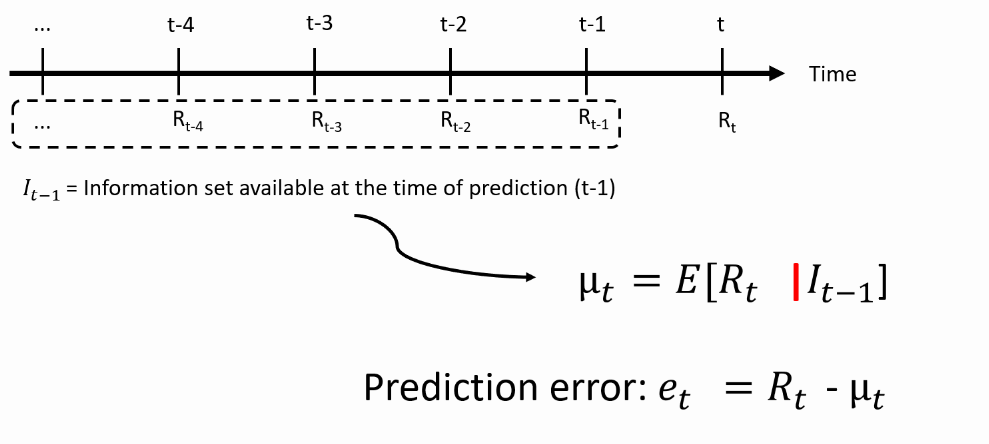
  • At time $t-1$, you make the prediction about the the future return $R_t$, using the information set available at time $t-1$:

Predicted volatilities

GARCH Models in R

Notation (iii)

  • Predicting the mean return: what is the best possible prediction of the actual return? Predicted volatilities
GARCH Models in R

Notation (iv)

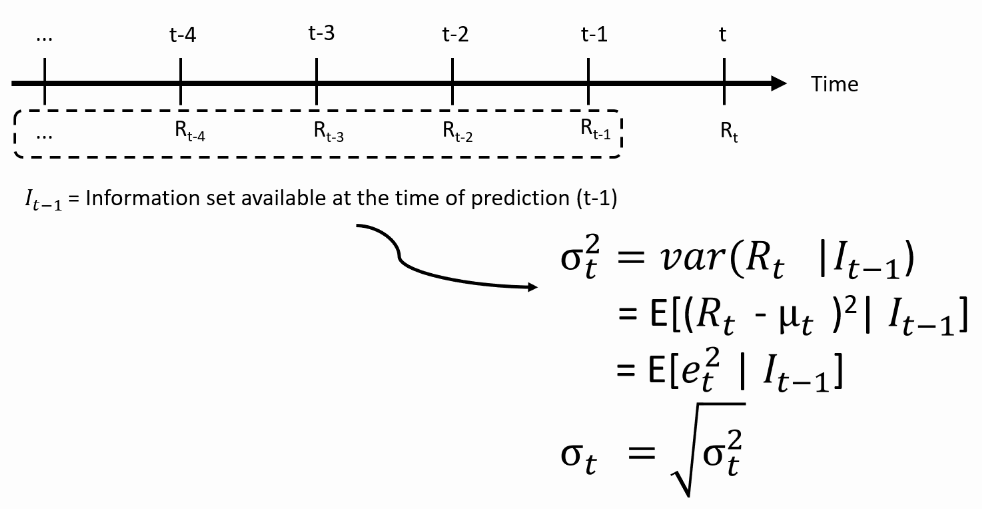
  • We then predict the variance: how far off the return can be from its mean? Predicted volatilities
GARCH Models in R

From theory to practice: Models for the mean

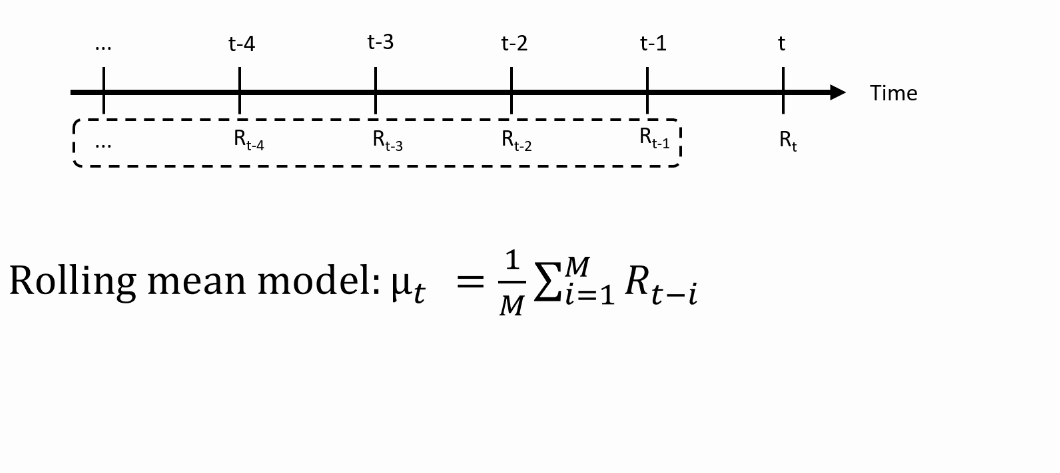
  • We need an equation that maps the past returns into a prediction of the mean Predicted volatilities

For AR(MA) models for the mean, see Datacamp course on time series analysis.

GARCH Models in R

From theory to practice: Models for the variance

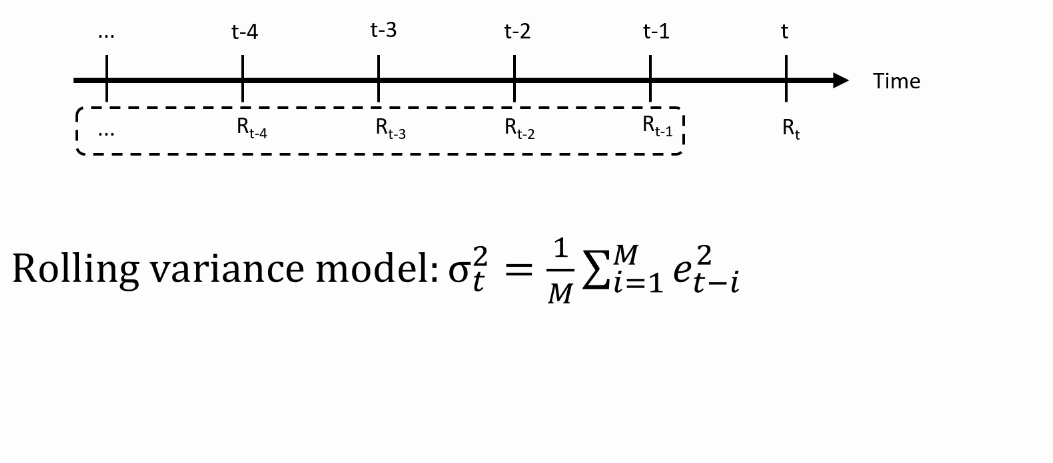
  • We need an equation that maps the past returns into predictions of the variance Predicted volatilities
GARCH Models in R

ARCH(p) model: Autoregressive Conditional Heteroscedasticity

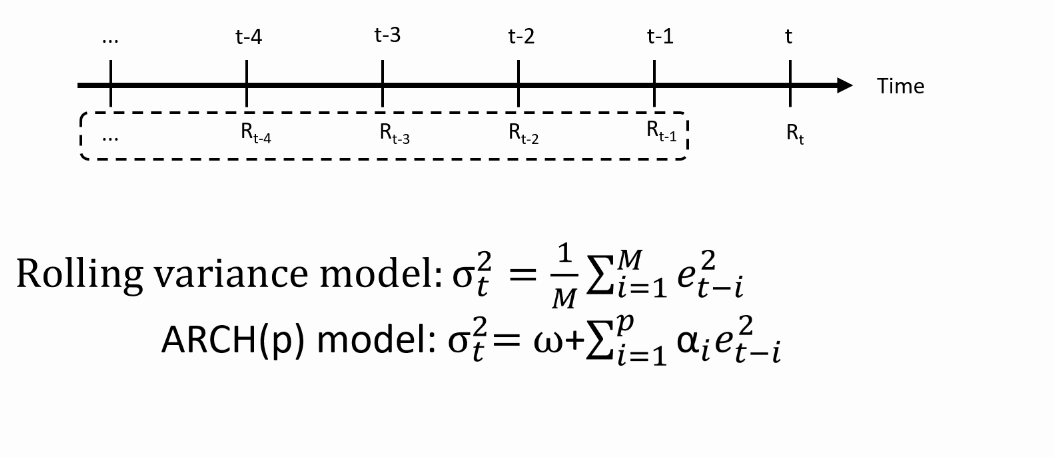
  • We need an equation that maps the past returns into predictions of the variance Predicted volatilities
GARCH Models in R

GARCH(1,1) model: Generalized ARCH

  • We need an equation that maps the past returns into predictions of the variance Predicted volatilities
GARCH Models in R

Parameter restrictions

To make the GARCH process realistic, we need that:

  1. $\omega$, $\alpha$ and $\beta$ are $>0$: this ensures that $\sigma^2_t >0$ at all times.

  2. $\alpha + \beta < 1$: this ensures that the predicted variance $\sigma^2_t$ always returns to the long run variance:

    • The variance is therefore "mean-reverting"
    • The long run variance equals $ \frac{\omega}{1-\alpha-\beta}$
GARCH Models in R

R implementation - Specify the inputs

  • Let's familiarize ourselves with the GARCH equations using R code:

$$ \sigma^{2}_{t} = \omega + \alpha e^{2}_{t-1} \beta \sigma^{2}_{t-1} $$

# Set parameter values
alpha <- 0.1
beta <- 0.8
omega <- var(sp500ret) * (1 - alpha - beta)
# Then: var(sp500ret) = omega / (1 - alpha - beta)

# Set series of prediction error
e <- sp500ret - mean(sp500ret) # Constant mean
e2 <- e ^ 2
GARCH Models in R

R implementation - compute predicted variances

# We predict for each observation its variance. 
nobs <- length(sp500ret)
predvar <- rep(NA, nobs)

# Initialize the process at the sample variance
predvar[1] <- var(sp500ret)

# Loop starting at 2 because of the lagged predictor
for (t in 2:nobs){
   predvar[t] <- omega + alpha * e2[t - 1] + beta * predvar[t-1]
}
GARCH Models in R

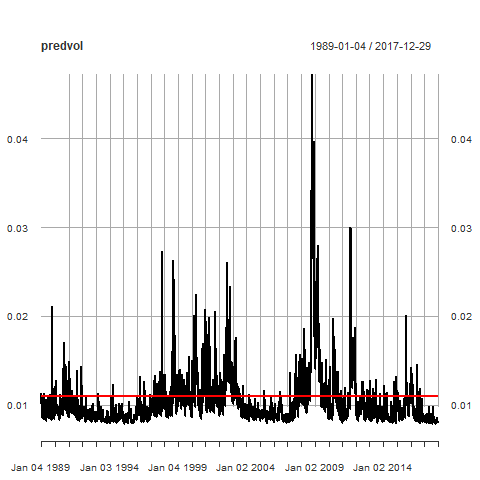
R implementation - Plot of GARCH volatilities

# Volatility is sqrt of predicted variance
predvol <- sqrt(predvar)
predvol <- xts(predvol, order.by = time(sp500ret))

# We compare with the unconditional volatility
uncvol <- sqrt(omega / (1 - alpha-beta))
uncvol <- xts(rep(uncvol, nobs), order.by = time(sp500ret))

# Plot
plot(predvol)
lines(uncvol, col = "red", lwd = 2)
GARCH Models in R

Predicted volatilities

GARCH Models in R

Let's practice!

GARCH Models in R

Preparing Video For Download...