Markets take the stairs up, but the elevator down

GARCH Models in R

Kris Boudt

Professor of finance and econometrics

How?

Change the argument distribution.model of ugarchspec() from "norm" to "sstd":

garchspec <- ugarchspec( mean.model = list(armaOrder = c(0, 0)),
                         variance.model = list(model = "sGARCH"),
                         distribution.model = "norm")

$$ \downarrow$$

garchspec <- ugarchspec( mean.model = list(armaOrder = c(0, 0)),
                         variance.model = list(model = "sGARCH"),
                         distribution.model = "sstd")

The normal GARCH model

Under the model assumptions

$$ R_{t} = \mu_{t} + e_{t} $$ $$ e_{t} \sim N(0, \sigma^{2}_{t}) $$

it follows that

$$ \frac{R_{t} - \mu_{t}}{\sigma_{t}} \sim N(0, 1) $$

Let's test

Caveat: The normality of the standardized returns follows from an assumption
Let's compute the standardized returns and test whether the assumption is correct.

Estimated standardized returns

Formula

$$ Z_{t} = \frac{R_{t} - \hat{\mu_{t}}}{ \hat{\sigma_{t}}} $$

Calculation in R

# Obtain standardized returns
stdret <- residuals(garchfit, standardize = TRUE)

Testing the normality assumption

library(PerformanceAnalytics)
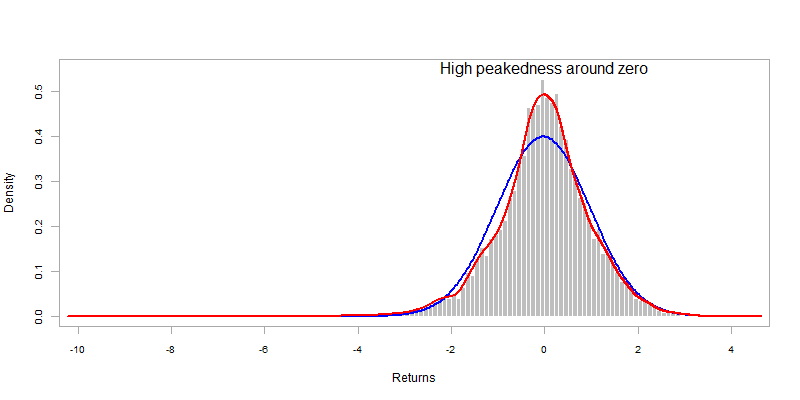
chart.Histogram(sp500ret, methods = c("add.normal", "add.density"),
          colorset = c("gray", "red", "blue"))

tails

Solution

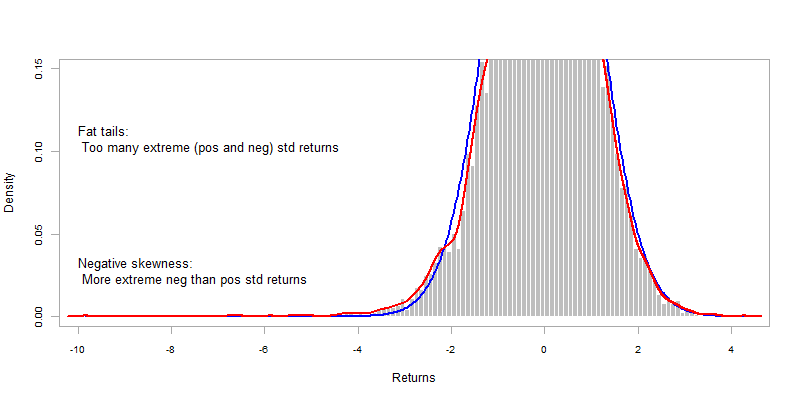
A realistic distribution thus needs to accommodate the presence of
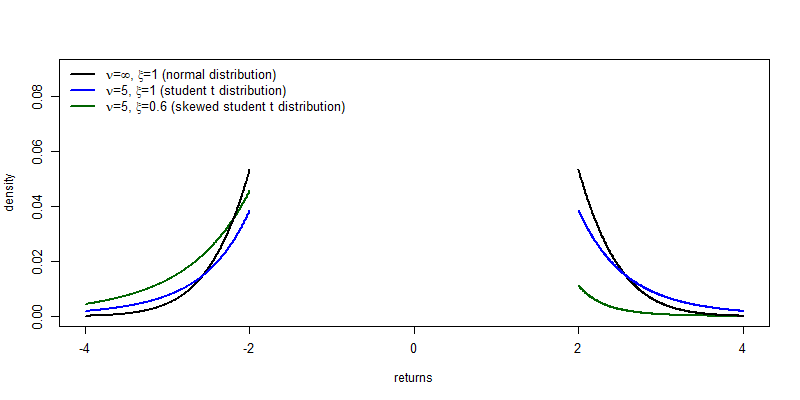
- fat tails: higher probability to observe large (positive or negative) returns than under the normal distribution
- skewness: asymmetry of the return distribution
In rugarch this is possible with the skewed student t distribution:

garchspec <- ugarchspec(distribution.model = "sstd")

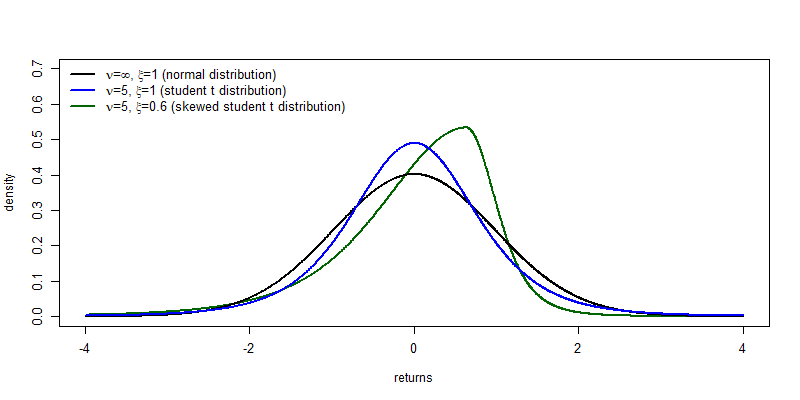
Parameters of the skewed student t distribution

Compared to the normal distribution, the skewed student t distribution has two extra parameters:
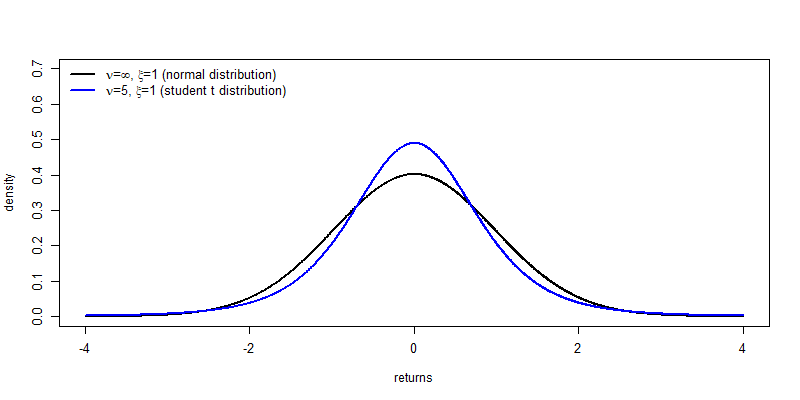
- Degrees of freedom parameter $\nu$ (in rugarch: shape): the lower is $\nu$ the fatter the tails.
- Skewness parameter $\xi$ (in rugarch: skew) : when $\xi=1$: symmetry. When $\xi<1$: negative skewness. For $\xi>1$: positive skewness.
Special cases:
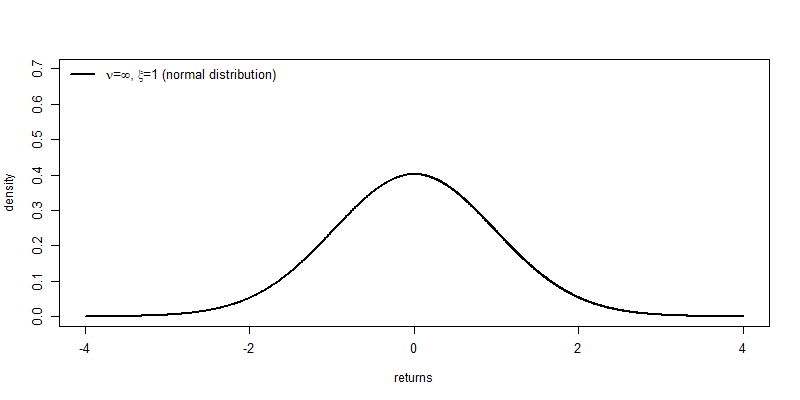
- When $\nu=\infty$ and $\xi=1$: normal distribution.
- When $\xi=1$: student t distribution.

GARCH model estimation with skewed student t

Set argument distribution.model to "sstd"

garchspec <- ugarchspec(mean.model = list(armaOrder = c(0,0)),
                        variance.model = list(model = "sGARCH"),
                        distribution.model = "sstd")

Estimate the model

garchfit <- ugarchfit(data = sp500ret, spec = garchspec)
coef(garchfit)

          mu        omega       alpha1        beta1         skew        shape 
5.669200e-04 6.281258e-07 7.462984e-02 9.223701e-01 9.436331e-01 6.318621e+00

Let's practice!

GARCH Models in R