GARCH volatility leads to time-varying variability of the returns

GARCH Models in R

Kris Boudt

Professor of finance and econometrics

GARCH covariance

If two asset returns $R_{1,t}$ and $R_{2,t}$ have correlation $\rho$ and time varying volatility $\sigma_{1,t}$ and $\sigma_{2,t}$, then their covariance is:

$$ \sigma_{12, t} = \rho \sigma_{1, t} \sigma_{2, t} $$

GARCH covariance estimation in four steps

Step 1: Use ugarchfit() to estimate the GARCH model for each return series.

msftgarchfit <- ugarchfit(data = msftret, spec = garchspec) 
wmtgarchfit <- ugarchfit(data = wmtret, spec = garchspec)

Step 2: Use residuals() to compute the standardized returns.

stdmsftret <- residuals(msftgarchfit, standardize = TRUE)
stdwmtret <- residuals(wmtgarchfit, standardize = TRUE)

Step 3: Use cor() to estimate $\rho$ as the sample correlation of the standardized returns.

msftwmtcor <- as.numeric(cor(stdmsftret, stdwmtret)) # equals 0.298795

GARCH covariance estimation in four steps

Step 4: Compute the GARCH covariance by multiplying the estimated correlation and volatilities

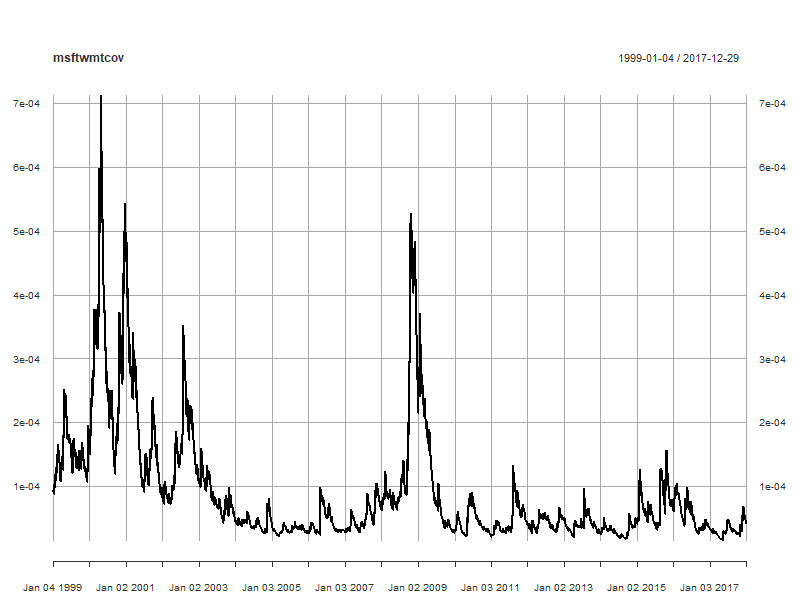
msftwmtcov <- msftwmtcor * sigma(msftgarchfit) * sigma(wmtgarchfit)

GARCH covariance

Applications of covariance in finance

Numerous!
Important case: Optimizing the variance of the portfolio.
It depends on the:
- portfolio weights
- the variance of all the assets
- the covariance between the asset returns

Application to portfolio optimization

Variance of portfolio of two assets with weight $w_{1,t}$ invested in asset 1 and $(1-w_{1,t})$ in asset 2:

$$ \sigma^{2}_{p, t} = w^{2}_{1, t} \sigma^{2}_{1, t} + (1 - w_{1, t})^{2} \sigma^{2}_{2, t} + 2 w_{1, t} (1 - w_{1, t}) \sigma_{12, t} $$

Many ways to define optimal $w_{1,t}$. One approach is to set $w_{1,t}$ such that the portfolio variance $\sigma_{t}^2$ is minimized.

First order condition to find minimum variance portfolio:

$$ \frac{\partial \sigma^{2}_{p, t}}{\partial w_{1, t}} = 2 w_{1, t} (\sigma^{2}_{1, t} + \sigma^{2}_{2, t} - 2 \sigma_{12, t}) - 2 (\sigma^{2}_{2, t} - \sigma_{12, t}) = 0 $$

Minimum variance portfolio weights

Solution: Min variance weights

Calculation in R:

msftvar <- sigma(msftgarchfit) ^ 2
wmtvar <- sigma(wmtgarchfit) ^ 2
msftwmtcov <- msftwmtcor * sigma(msftgarchfit) * sigma(wmtgarchfit)
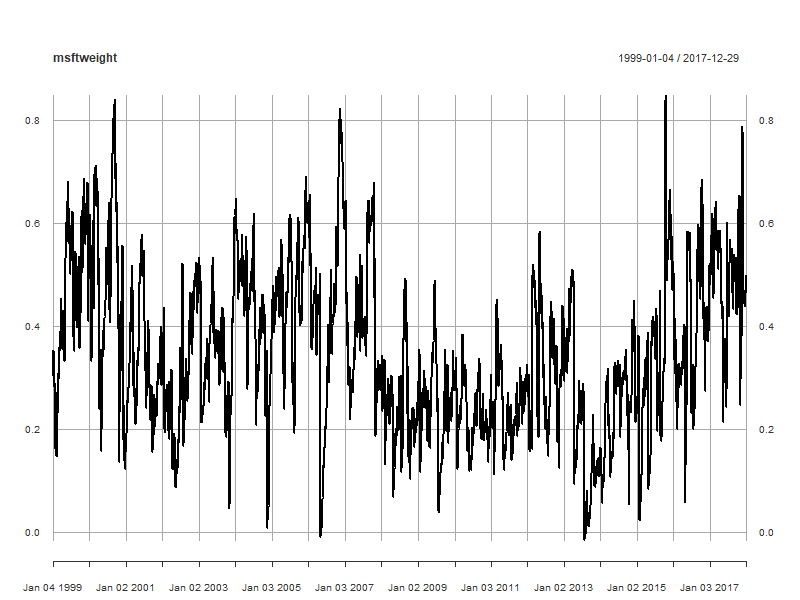
msftweight <- (wmtvar - msftwmtcov) / (msftvar + wmtvar - 2 * msftwmtcov)

GARCH covariance

Dynamic beta

The estimation of a stock's beta is the systematic risk of a stock

Defined as the covariance of the stock return and the market return, divided by the variance of the market returns

$$ \beta_{t} = \frac{\textnormal{covariance between the stock return and the market return}}{\textnormal{variance of the market return}} $$

Needed to compute the risk premium. The higher it is, the more risky the stock and thus the higher the required rate of return.

For US stocks, the market return is the return on the S&P 500.

The daily beta of MSFT

Compute the covariance between MSFT and S&P 500 returns

msftsp500cor <- as.numeric(cor(stdmsftret, stdsp500ret))
msftsp500cov <- msftsp500cor * sigma(msftgarchfit) * sigma(sp500garchfit)

Compute the variance of the S&P 500 returns

sp500var <- sigma(sp500garchfit) ^ 2

Compute the beta

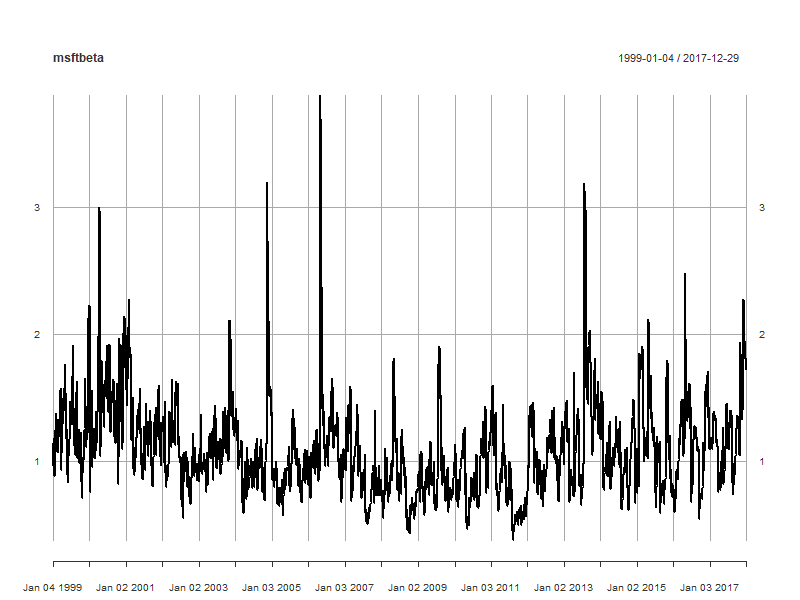
msftbeta <- msftsp500cov / sp500var

MSFT beta

Let's practice!

GARCH Models in R