Avoid unnecessary complexity

GARCH Models in R

Kris Boudt

Professor of finance and econometrics

Avoid unneeded complexity

If you know
- The mean dynamics are negligible
- There is no leverage effect in the variance
- The distribution is symmetric and fat-tailed

Then a constant mean, standard GARCH(1, 1) with student t distribution is an appropriate specification to use:

garchspec <- ugarchspec(mean.model = list(armaOrder = c(0, 0)),
                        variance.model = list(model = "sGARCH"),
                        distribution.model = "std")

Restrict the parameter estimates

If you know that the parameters
- are equal to a certain value
- or, are inside an interval
Then you should impose this in the specification using the methods
- setfixed()
- setbounds()

Application to exchange rates

Specification and estimation

garchspec <- ugarchspec(mean.model = list(armaOrder = c(0, 0)),
                        variance.model = list(model = "sGARCH"),
                        distribution.model = "std")
garchfit <- ugarchfit(data = EURUSDret, spec = garchspec)

Estimation results

coef(garchfit)

           mu         omega        alpha1         beta1         shape 
-3.562136e-05  8.005123e-08  3.097322e-02  9.674496e-01  8.821902e+00

Example of setfixed()

If you know alpha1 = 0.05 and shape = 6: impose those values in the estimation.
How? Use of setfixed() method on a ugarchspec object

setfixed(garchspec) <- list(alpha1 = 0.05, shape = 6)

Result

garchfit <- ugarchfit(data = EURUSDret, spec = garchspec)

coef(garchfit)

           mu         omega        alpha1         beta1         shape 
-4.142922e-05  2.061772e-07  5.000000e-02  9.489622e-01  6.000000e+00

Bounds on parameters

The GARCH parameters can be restricted to an interval.
Sometimes the interval of plausible values is large:
- To ensure the variance is positive, we require e.g. that all variance parameters ($\omega$, $\alpha$, $\beta$, $\gamma$) are positive.
Sometimes the interval of plausible values is smaller:
- Likely values of $\alpha$ are in between 0.05 and 0.2
- Likely values of $\beta$ are in between 0.7 and 0.95
Such bound constraints on the parameters can be imposed using the setbounds() method.

Example of setbounds()

setbounds(garchspec) <- list(alpha1 = c(0.05, 0.2), beta1 = c(0.8, 0.95))

Use your intuition to avoid unneeded complexity.

Use the information you have:

to build simple (and smart) models
to fix parameter values or set bounds
to make the GARCH dynamics realistic:
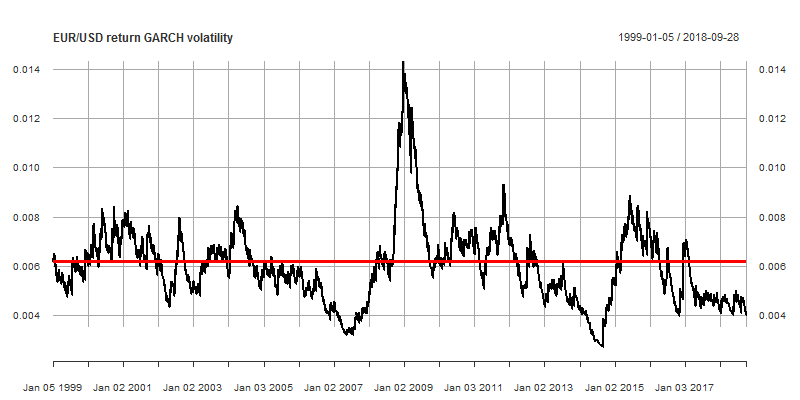
- mean reversion of the volatility around the sample standard deviation
```
sd(EURUSDret) # returns a value of 0.006194049
```

Volatility clusters and mean reversion of volatility

Variance targeting

Mathematically, this means that the unconditional variance implied by the GARCH models equals the sample variance $\hat \sigma^2$.
How? By setting the argument variance.targeting = TRUE in variance.model of ugarchspec():

garchspec <- ugarchspec(mean.model = list(armaOrder = c(0,0)),
                        variance.model = list(model = "sGARCH",
                        variance.targeting = TRUE),
                        distribution.model = "std")
garchfit <- ugarchfit(data = EURUSDret, spec = garchspec)
all.equal(uncvariance(garchfit), sd(EURUSDret) ^ 2, tol = 1e-4)

TRUE

Let's impose restrictions on the GARCH model

GARCH Models in R