The rugarch package

GARCH Models in R

Kris Boudt

Professor of finance and econometrics

The normal GARCH(1,1) model with constant mean

The normal GARCH model

$$ R_t = \mu + e_t $$ $$ e_t \sim N(0, \sigma^2_t) $$ $$ \sigma^2_t = \omega + \alpha e^2_{t-1} + \beta \sigma^2_{t-1} $$

  • Four parameters: $\mu, \omega, \alpha, \beta$.
  • Estimation by maximum likelihood: find the parameter values for which the GARCH model is most likely to have generated the observed return series.
GARCH Models in R

Alexios Ghalanos

library(rugarch)
citation("rugarch")

To cite the rugarch package, please use:

Alexios Ghalanos (2018). rugarch: Univariate GARCH models.R package version 1.4-0.
GARCH Models in R

Workflow

  • Three steps:

    • ugarchspec(): Specify which GARCH model you want to use (mean $\mu_t$, variance $\sigma^2_t$, distribution of $e_t$)

      • ugarchfit(): Estimate the GARCH model on your time series with returns $R_1,...,R_T$.

      • ugarchforecast(): Use the estimated GARCH model to make volatility predictions for $R_{T+1}$,...

GARCH Models in R

Workflow in R

ugarchspec() specifies which GARCH model you want to use.

garchspec <- ugarchspec(mean.model = list(armaOrder = c(0,0)),
                           variance.model = list(model = "sGARCH"),
                           distribution.model = "norm")

ugarchfit() estimates the GARCH model.

garchfit <- ugarchfit(data = sp500ret, spec = garchspec)

ugarchforecast() forecasts the volatility of the future returns.

garchforecast <- ugarchforecast(fitORspec = garchfit, n.ahead = 5)
GARCH Models in R

ugarchfit object

  • The ugarchfit yields an object that contains all the results related to the estimation of the garch model.
  • Methods coef, uncvar, fitted and sigma: 
# Coefficients
garchcoef <- coef(garchfit)
# Unconditional variance
garchuncvar <- uncvariance(garchfit)
# Predicted mean
garchmean <- fitted(garchfit) 
# Predicted volatilities
garchvol <- sigma(garchfit)

GARCH Models in R

GARCH coefficients for daily S&P 500 returns

print(garchcoef)

          mu        omega       alpha1        beta1 
5.728020e-04 1.220515e-06 7.792031e-02 9.111455e-01

$$ R_{t} = 5.7 \times 10^{-4} + e_{t} $$ $$ e_{t} \sim N(0, \hat{\sigma}^{2}_{t}) $$ $$ \hat{\sigma}^{2}_{t} = 1.2 \times 10^{-6} + 0.08 e^{2}_{t-1} + 0.91 \hat{\sigma}^{2}_{t-1} $$

sqrt(garchuncvar)

0.01056519
GARCH Models in R

Estimated volatilities

garchvol <- sigma(garchfit)
plot(garchvol)

GARCH Models in R

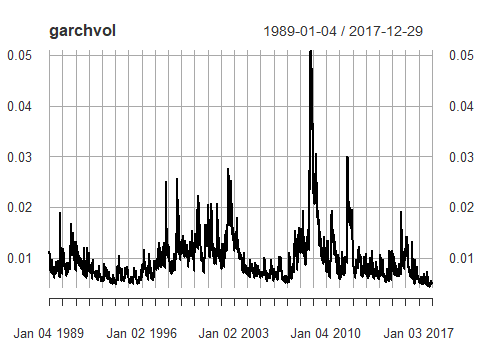
What about future volatility?

tail(garchvol, 1)

2017-12-29 0.004862908

What about the volatility for the days following the end of the time series?

GARCH Models in R

Forecasting h-day ahead volatilities

  • Applying the sigma() method to the ugarchforecast object gives the volatility forecasts:
sigma(garchforecast)

      2017-12-29
T+1  0.005034754
T+2  0.005127582
T+3  0.005217770
T+4  0.005305465
T+5  0.005390797
GARCH Models in R

Forecasting h-day ahead volatilities

Applying the fitted() method to the ugarchforecast object gives the mean forecasts:

fitted(garchforecast)

      2017-12-29
T+1  0.000572802
T+2  0.000572802
T+3  0.000572802
T+4  0.000572802
T+5  0.000572802
GARCH Models in R

Application to tactical asset allocation

A portfolio that invests a percentage $w$ in a risky asset (with volatility $\sigma_t$) and keeps $1-w$ on a risk-free bank deposit account has volatility equal to

$$ \sigma_p = w \sigma_t$$

How to set $w$? One approach is volatility targeting: $w$ is such that the predicted annualized portfolio volatility equals a target level, say 5%. Then:

$$ w^* = 0.05 /\sigma_t $$

Since GARCH volatilities change, the optimal weight changes as well.

GARCH Models in R

Let's play with rugarch!

GARCH Models in R

Preparing Video For Download...