Validate your assumptions about the mean and variance

GARCH Models in R

Kris Boudt

Professor of finance and econometrics

Check 1: Mean and standard deviation of standardized returns

Formula standardized returns

$$ Z_{t} = \frac{R_{t} - \hat{\mu_{t}}}{ \hat{\sigma_{t}}} $$

  • First check of model validity:
    • Sample mean of standardized returns $\approx$ 0
    • Sample standard deviation of standardized returns $\approx$ 1
GARCH Models in R

Check 2: Time series plot of standardized returns

  • Second check of model validity:
    • time series plot of standardized returns
    • standardized returns should have constant variability
GARCH Models in R

GARCH Models in R

GARCH Models in R

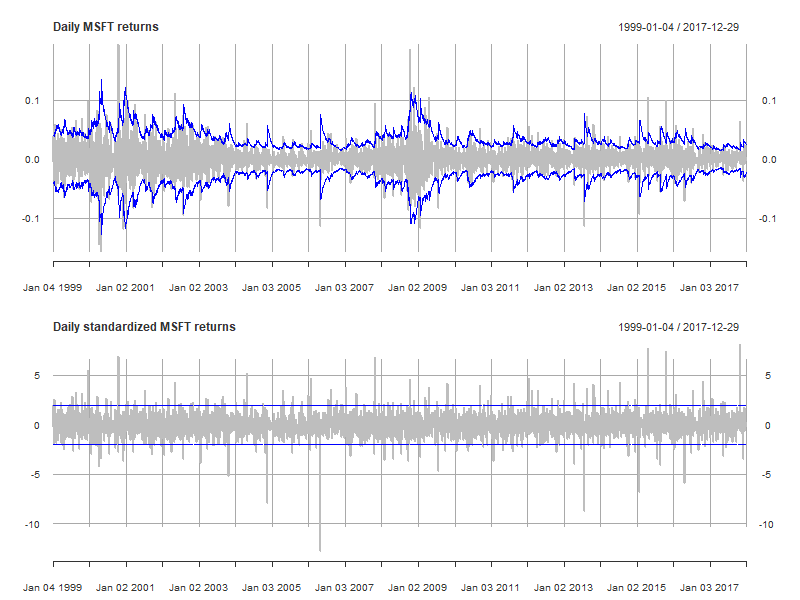
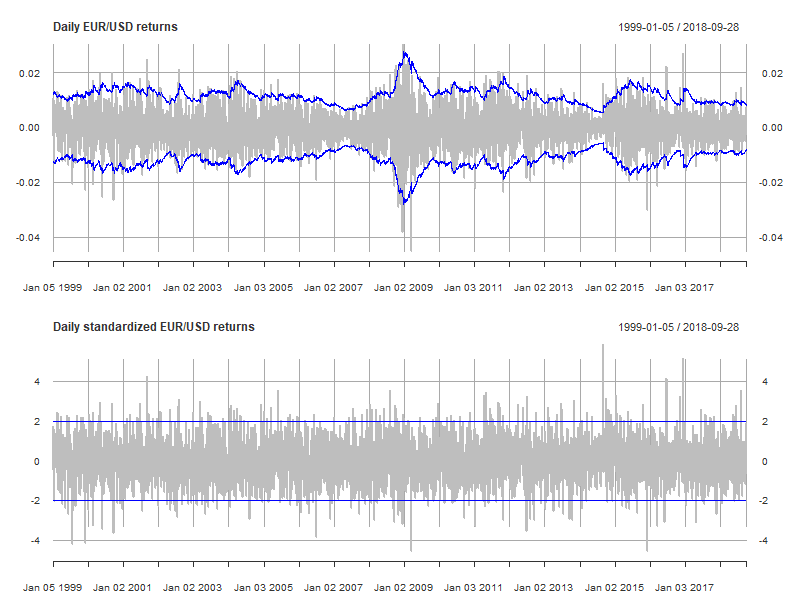
Check 3: No predictability in the absolute standardized returns

  • Third check of model validity:

    • verify that there is no correlation between the past absolute standardized return and the current absolute standardized return.
    • this means: $ Corr(|Z_{t-k}|, |Z_{t}|) \approx 0, $ for $k>0$

  • Why?

    • The magnitude of the absolute standardized return should be constant $\rightarrow$ no correlations in the absolute standardized returns.
GARCH Models in R

Autocorrelations

  • Such within time series correlations are called autocorrelations of order k
    • $k=1$: $Corr(|Z_{t-1}|, |Z_{t}|)$: Correlation of the current absolute standardized return and its previous value.
    • $k=2$: $Corr(|Z_{t-2}|, |Z_{t}|)$: Correlation of the current absolute standardized return and its value two periods ago.
    • ...
  • All of these should be 0. Except:
    • $k=0$: $Corr(|Z_{t}|, |Z_{t}|)$: Correlation of the absolute standardized return with itself: equals 1.
GARCH Models in R

acf()

  • In R, we can compute those autocorrelations using the autocorrelation function denoted by acf()
    • Input: Time series, maximum order
    • Output: The correlogram: plot showing the values of the autocorrelation for different orders $k = 0, 1, ...$.
GARCH Models in R

Application to MSFT

garchspec <- ugarchspec(mean.model = list(armaOrder = c(1, 0)),
                        variance.model = list(model = "gjrGARCH"),
                        distribution.model = "sstd")
garchfit <- ugarchfit(data = msftret, spec = garchspec)
stdmsftret <- residuals(garchfit, standardize = TRUE)

acf(abs(msftret), 22)
acf(abs(stdmsftret), 22)
GARCH Models in R

GARCH Models in R

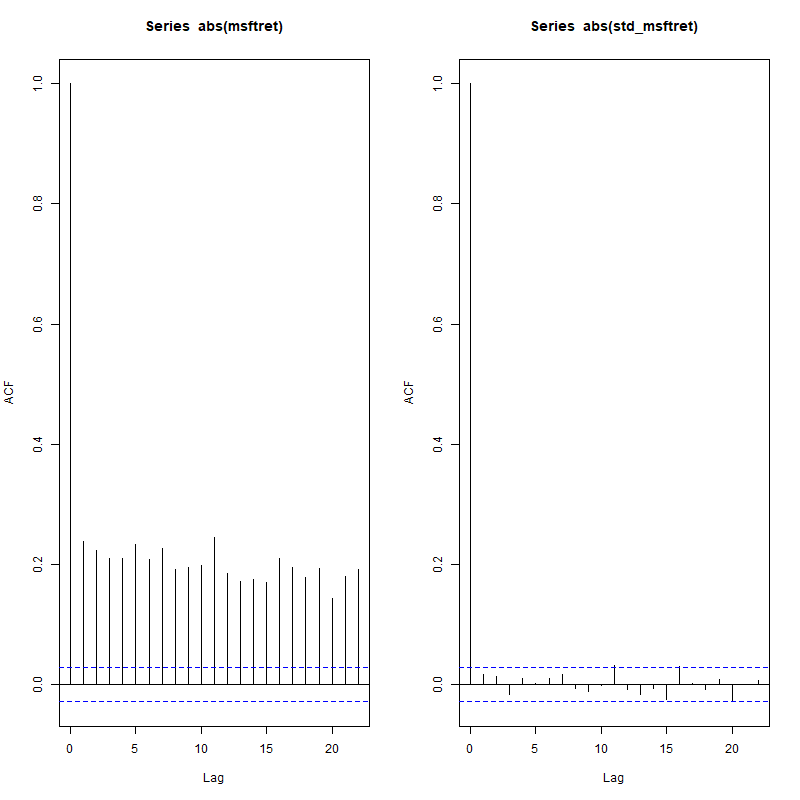
Check 4: Ljung-Box test

  • Fourth check of model validity:
    • Ljung-Box test that the first k autocorrelations in the absolute standardized returns $|Z_t$| are zero: $$ H_0: Corr(|Z_t|,|Z_{t-1}|) = Corr(|Z_t|,|Z_{t-2}|) = ... = Corr(|Z_t|,|Z_{t-k}|) = 0 $$
    • Similar to a $t$-test for statistical significance of the estimated parameters, but here we want to have 0 in order to have a good model.

Rule of thumb: p-value less than 5% indicates that the model used is not valid.

GARCH Models in R

Ljung-Box test in R

  • In R: function Box.test() with 3 arguments:
    • series
    • maximum order for which autocorrelations are zero
    • type = "Ljung-Box"

Example: 

Box.test(abs(stdmsftret), 22, type = "Ljung-Box")
  • Output: p-value
    • Rule of thumb: p-value less than 5% indicates that the model used is not valid.
GARCH Models in R

Box.test using absolute standardized MSFT returns

Test on absolute standardized returns: 

Box.test(abs(stdmsftret), 22, type = "Ljung-Box")

    Box-Ljung test
data:  abs(stdmsftret)
X-squared = 25.246, df = 22, p-value = 0.2855

Note: p-value is 28.55% > 5%. We cannot reject that: $$ H_0: Corr(|Z_t|,|Z_{t-1}|) = Corr(|Z_t|,|Z_{t-2}|) = ... = Corr(|Z_t|,|Z_{t-22}|) = 0 $$

GARCH Models in R

Let's diagnose the absolute standardized returns.

GARCH Models in R

Preparing Video For Download...