Dimensions of portfolio performance

Introduction to Portfolio Analysis in R

Kris Boudt

Professor, Free University Brussels & Amsterdam

Interpretation of portfolio returns

ch_2_video_1.003.png

Interpretation of portfolio returns

ch_2_video_1.004.png

Interpretation of portfolio returns

ch_2_video_1.005.png

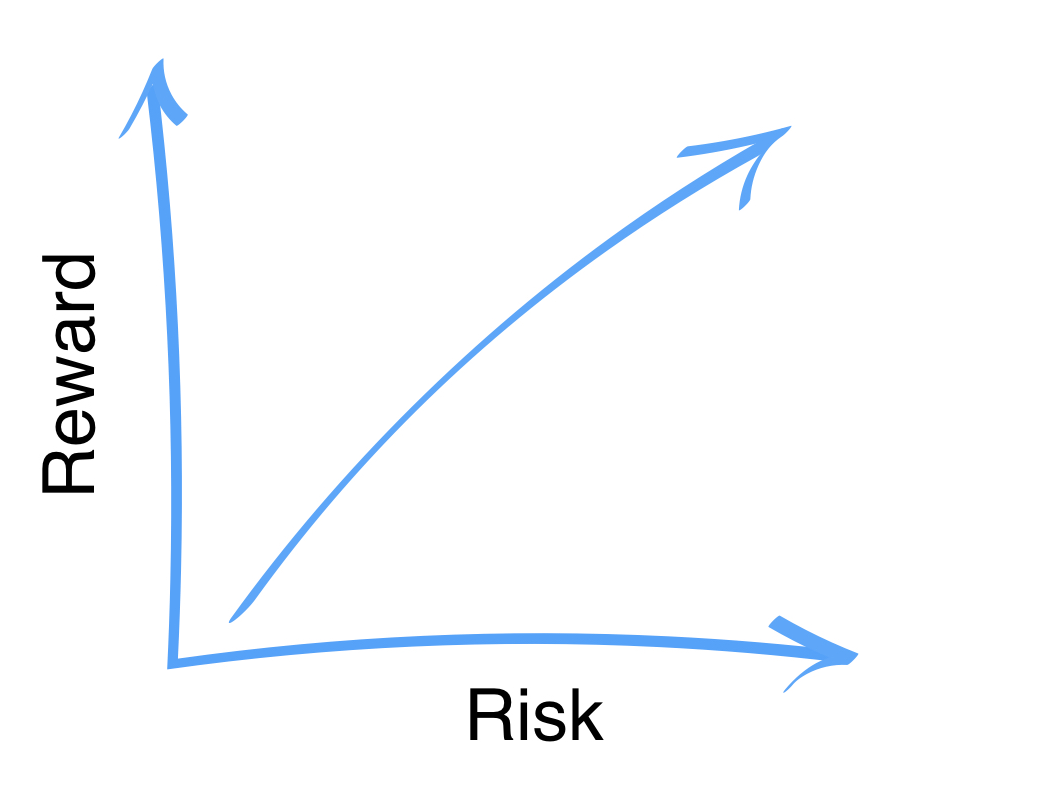
Risk vs. reward

ch_2_video_1.006.png

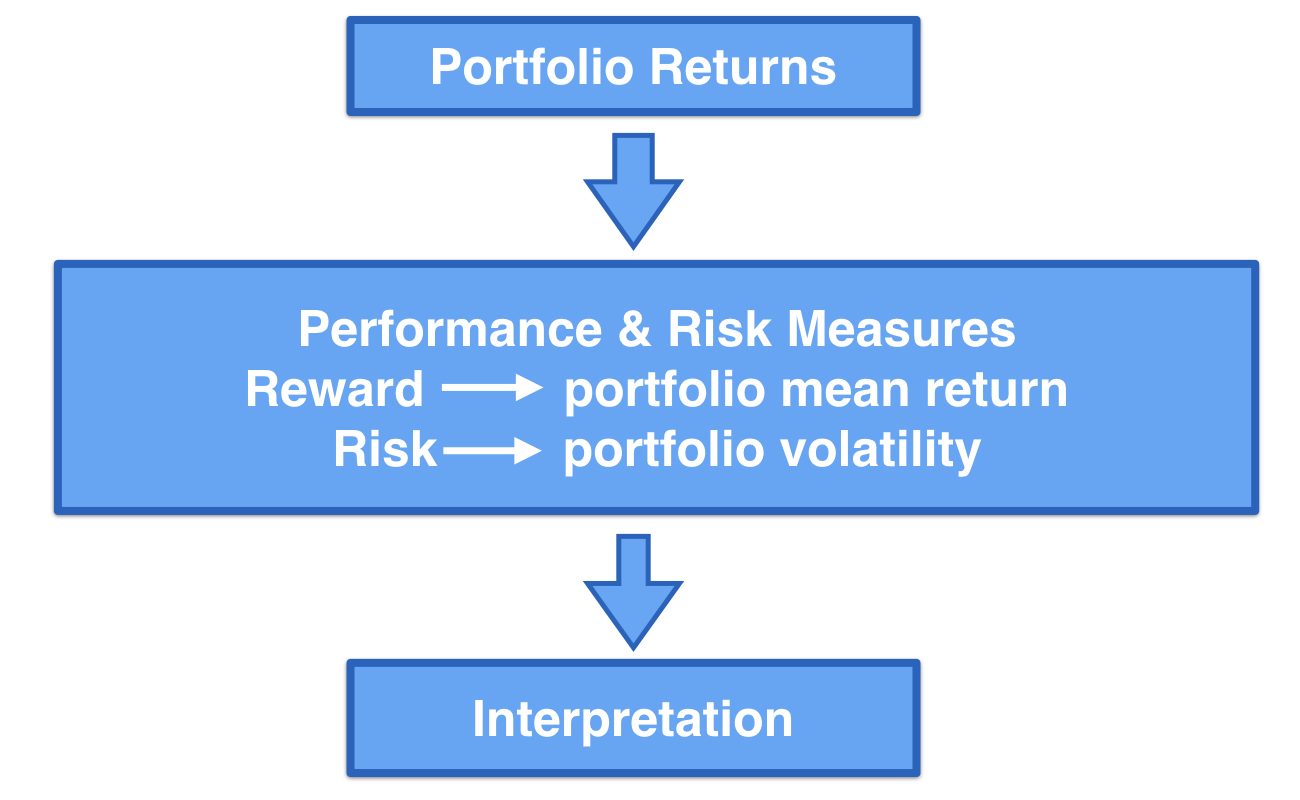
Need for performance measure

ch_2_video_1.007.png

Arithmetic mean return

Assume a sample of T portfolio return observations:
- $R_1 , R_2, ... , R_T$
Reward measurement: Arithmetic mean return is given:
- $\displaystyle \hat{\mu} = \frac{R_1 , R_2, ... , R_T}{T}$
It shows how large the portfolio return is on average

Risk: portfolio volatility

De-meaned return
- $R_i - \hat{\mu}$
Variance of the portfolio
- $\displaystyle \hat{\sigma}^2 = \frac{(R_1 - \hat{\mu})^2 + (R_2 - \hat{\mu})^2 + ... + (R_T - \hat{\mu})^2}{T_1}$
Portfolio volatility:
- $\displaystyle \hat{\sigma} = \sqrt{\hat{\sigma}^2}$

No linear compensation in return

Mismatch between average return and effective return

ch_2_video_1.018.png

No linear compensation in return

Mismatch between average return and effective return

No linear compensation in return

Mismatch between average return and effective return

ch_2_video_1.020.png

Geometric mean return

Formula for Geometric Mean for a sample of T portfolio return observations $R_1, R_2, ..., R_T$:

Geometric mean = $[(1+R_1)\cdot(1+R_2)\cdot...(1+R_T)]^{1/T} - 1$

Example: +50% & -50% return
- Geometric mean = $[(1+ 0.50)\cdot (1-0.50)]^{1/2} -1$
- = $0.75^{1/2} - 1$
- = -13.4%

Let's practice!

Introduction to Portfolio Analysis in R

Preparing Video For Download...