Non-normality of the return distribution

Introduction to Portfolio Analysis in R

Kris Boudt

Professor, Free University Brussels & Amsterdam

Volatility describes "normal" risk

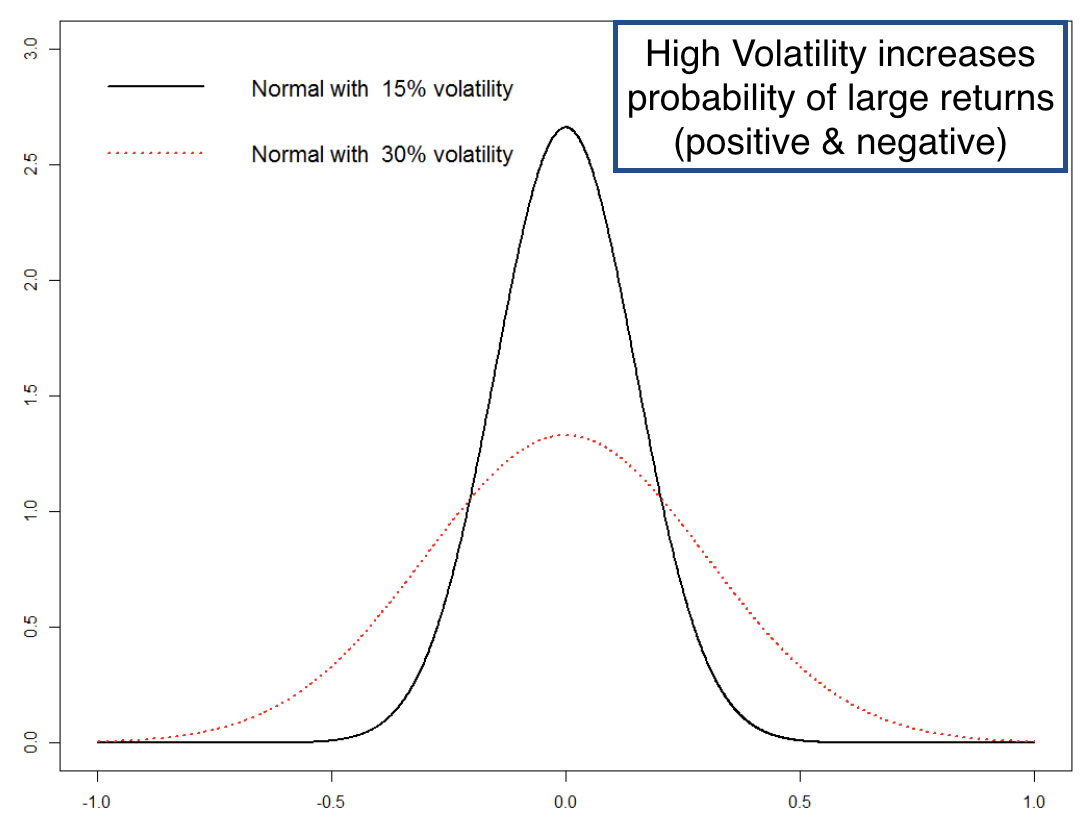
Screenshot 2019-08-21 at 11.56.34.png

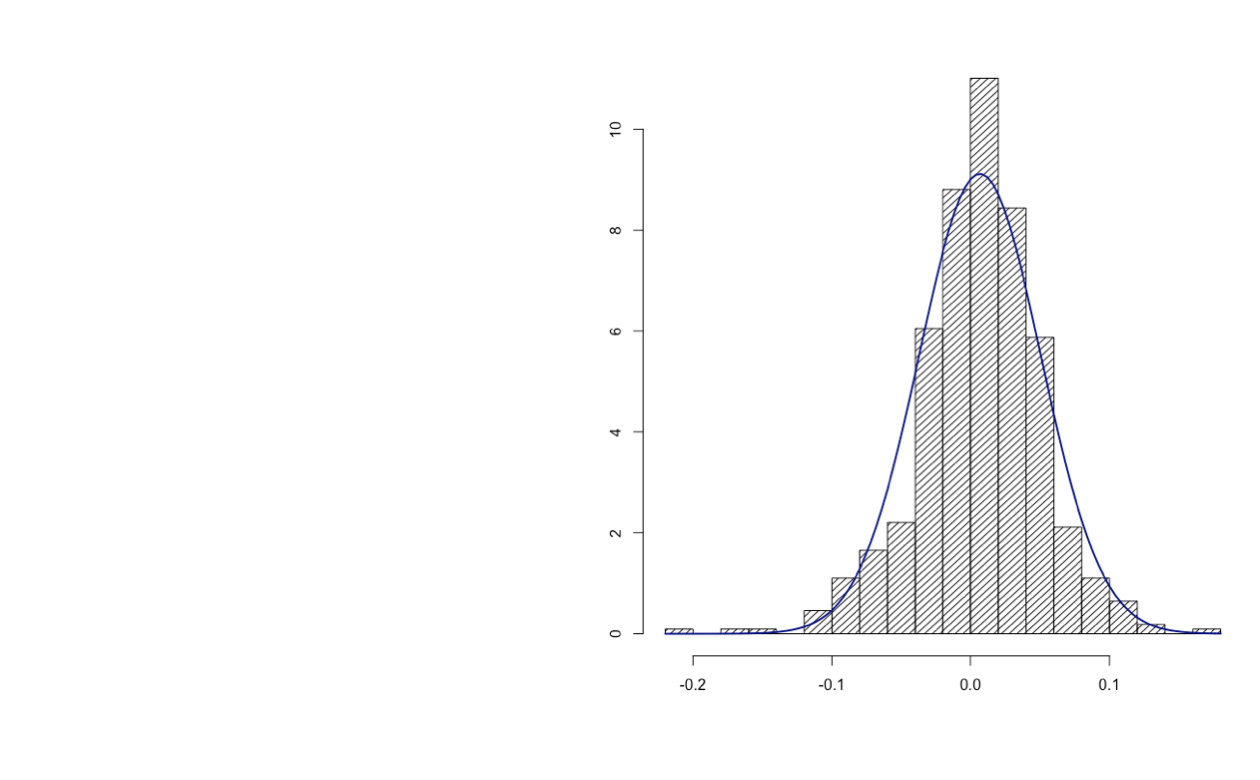
ch_2_video_4.001.png

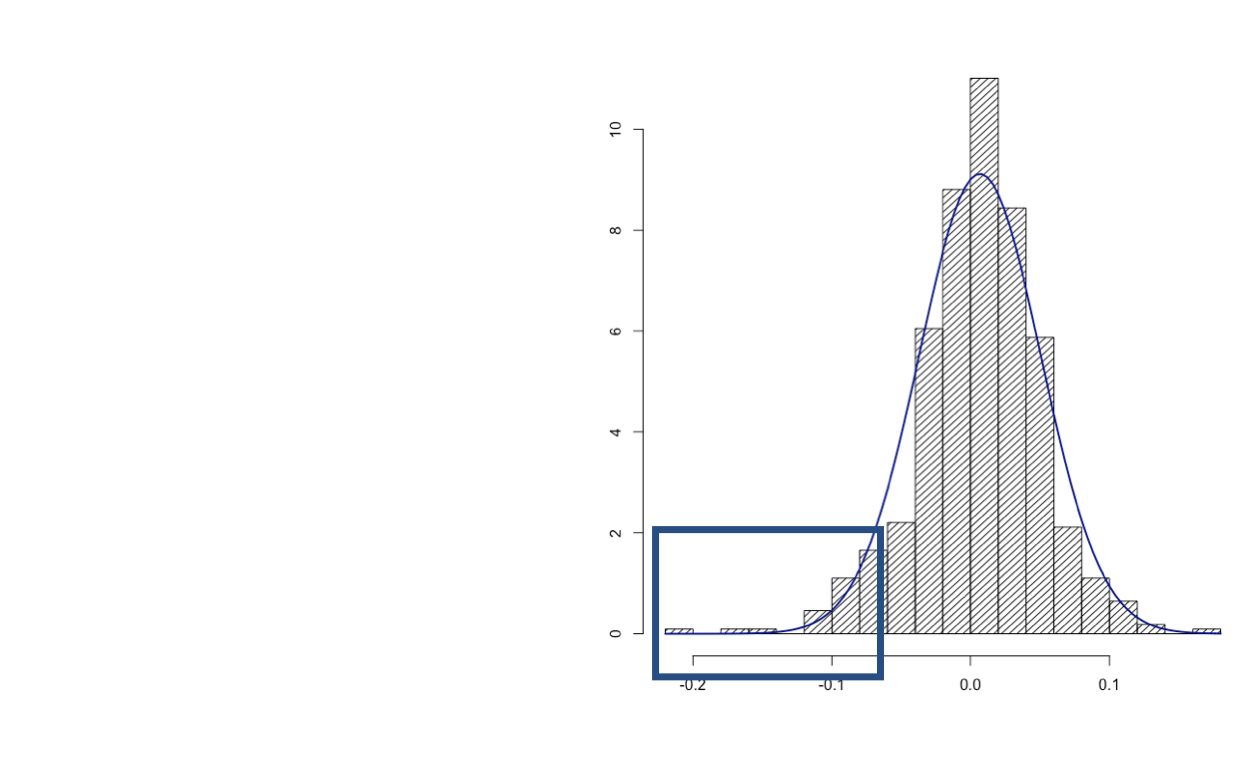
ch_2_video_4.002.png

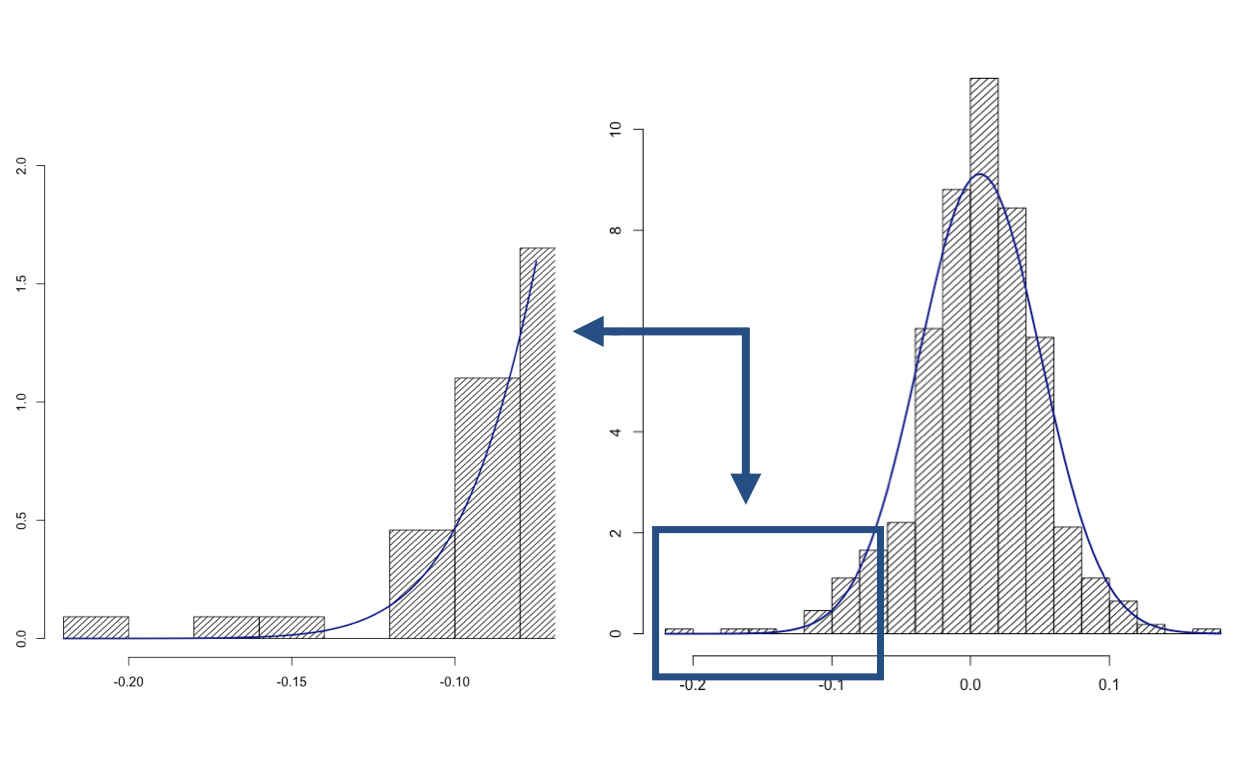
ch_2_video_4.003.png

Standard Deviation of portfolio returns:
- Take the full sample of returns
  
  $$SD = \sqrt{\frac{(R_1-\mu)^2 + (R_2-\mu)^2 + ... + (R_T-\mu)^2}{T-1}}$$
Semi-Deviation of portfolio returns:
- Take the subset of returns below the mean
  
  $$ SemiDev = \sqrt{\frac{(Z_1-\mu)^2 + (Z_2-\mu)^2 + ... + (Z_n-\mu)^2}{n}}$$

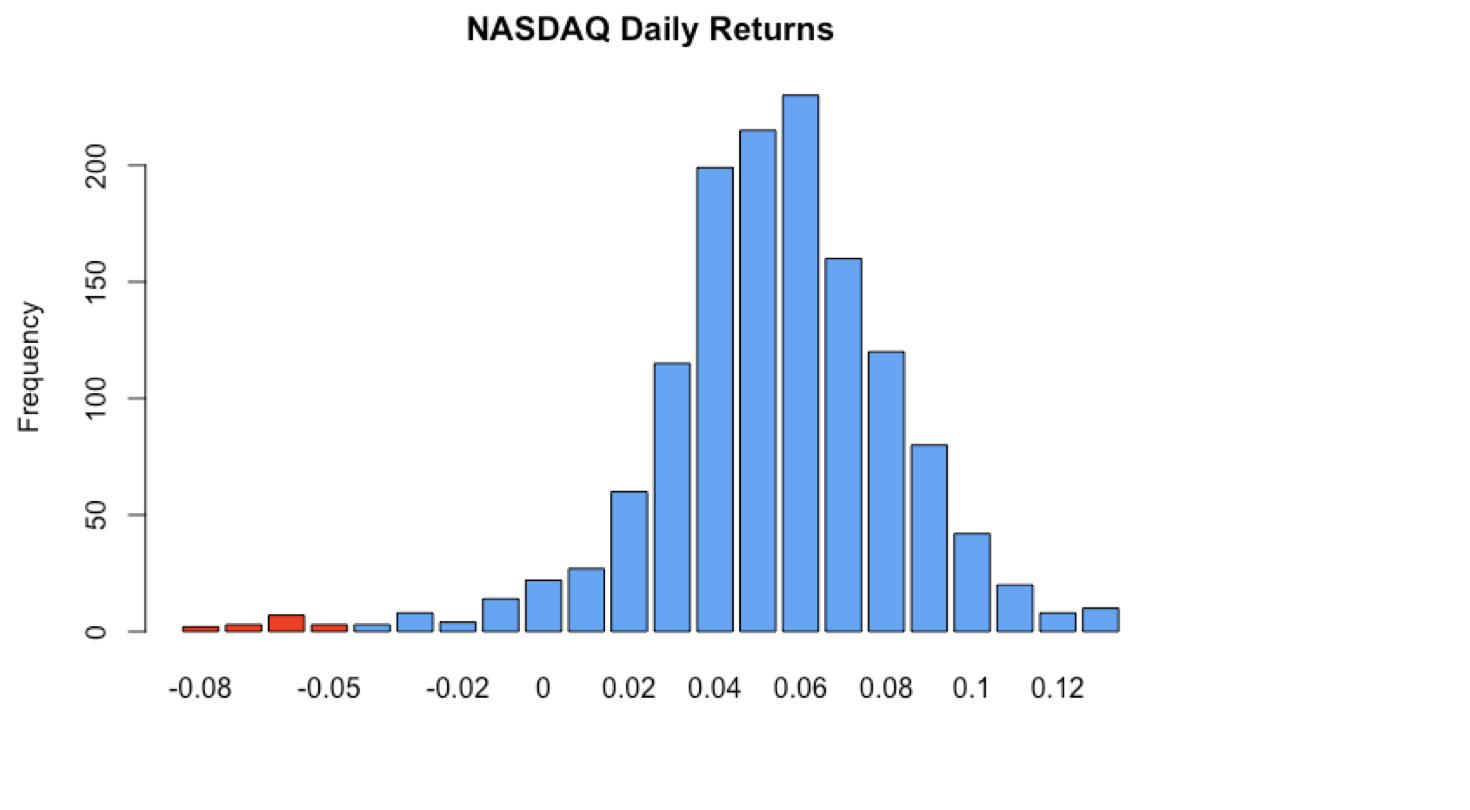
ch_2_video_4.012.png

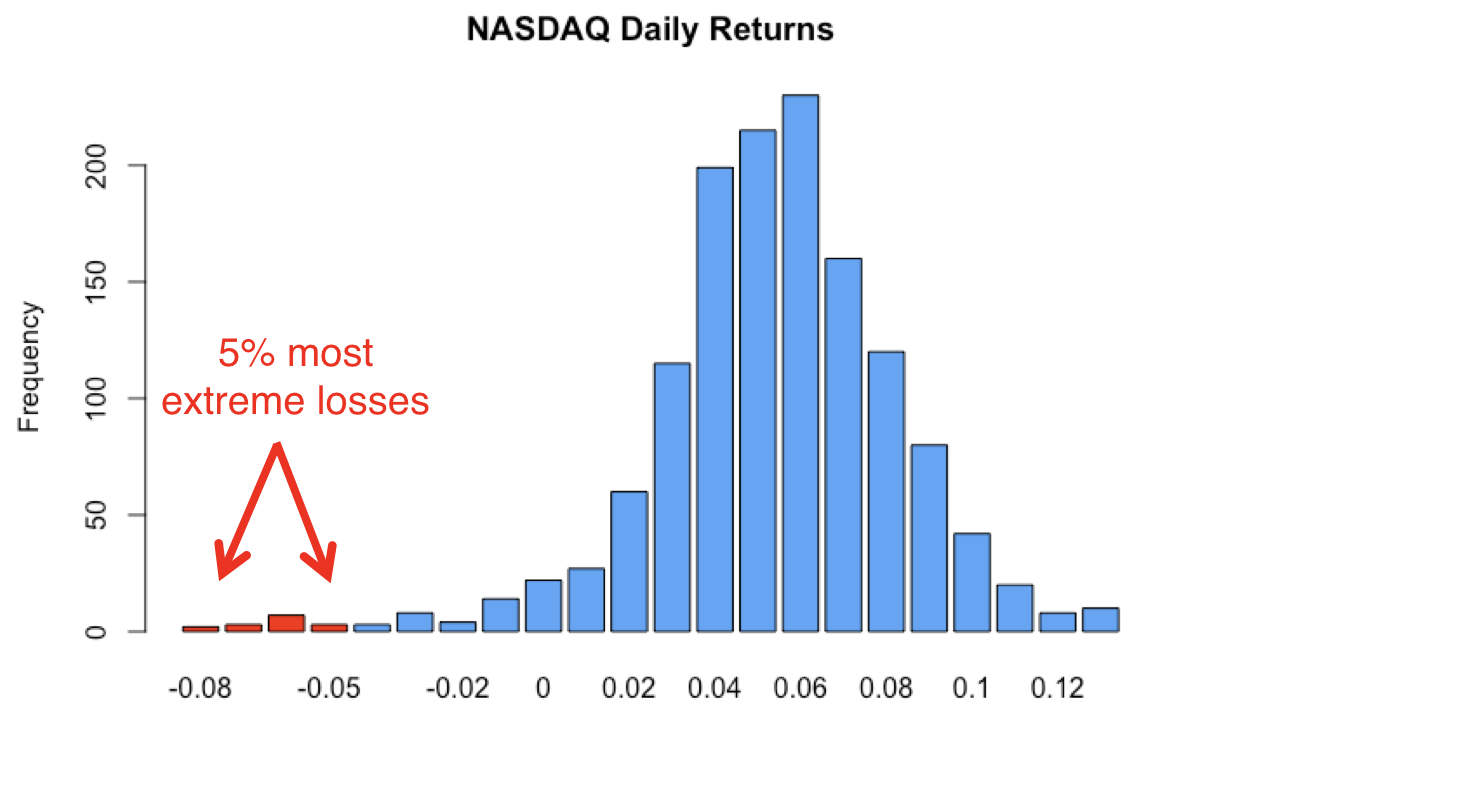
ch_2_video_4.013.png

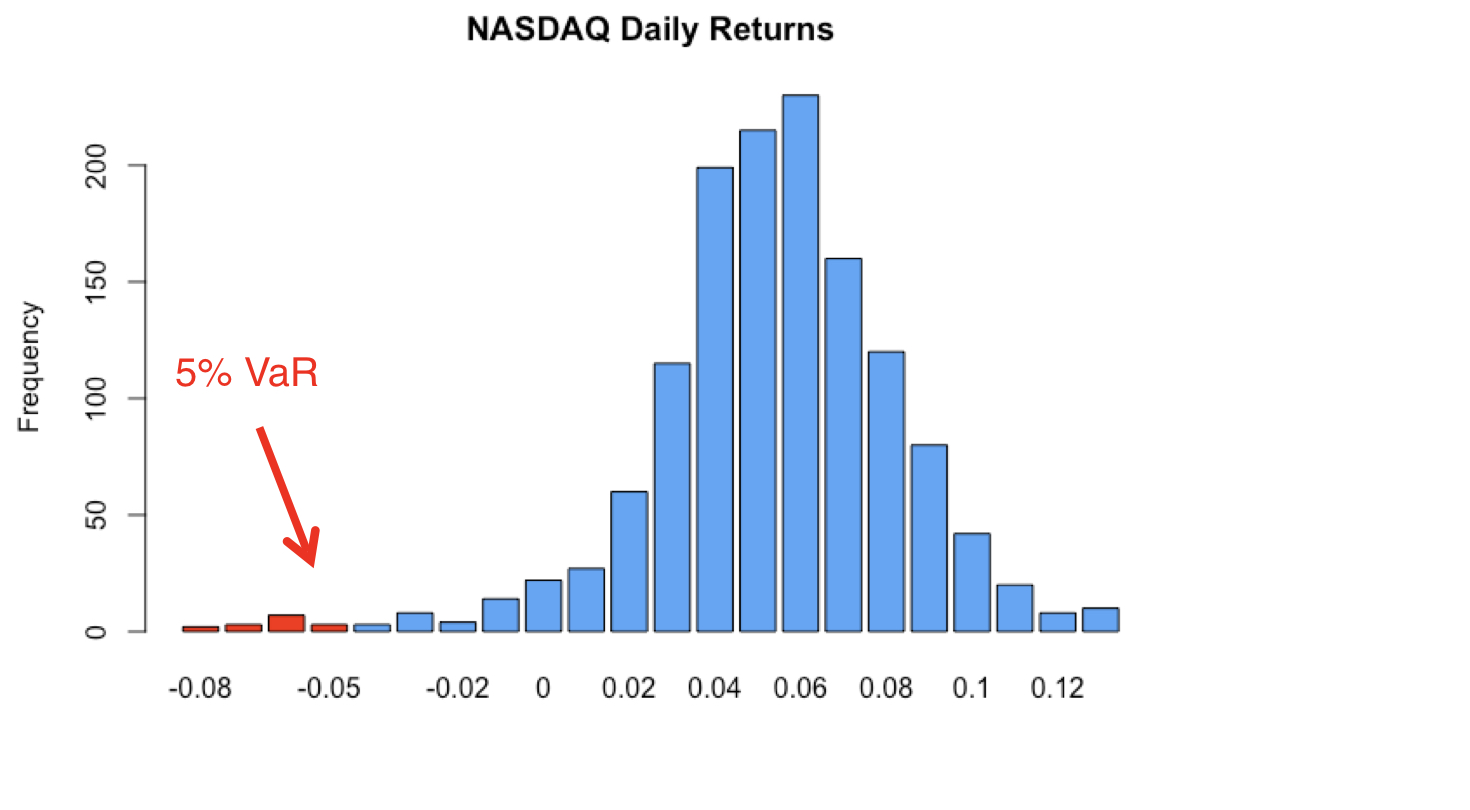
ch_2_video_4.015.png

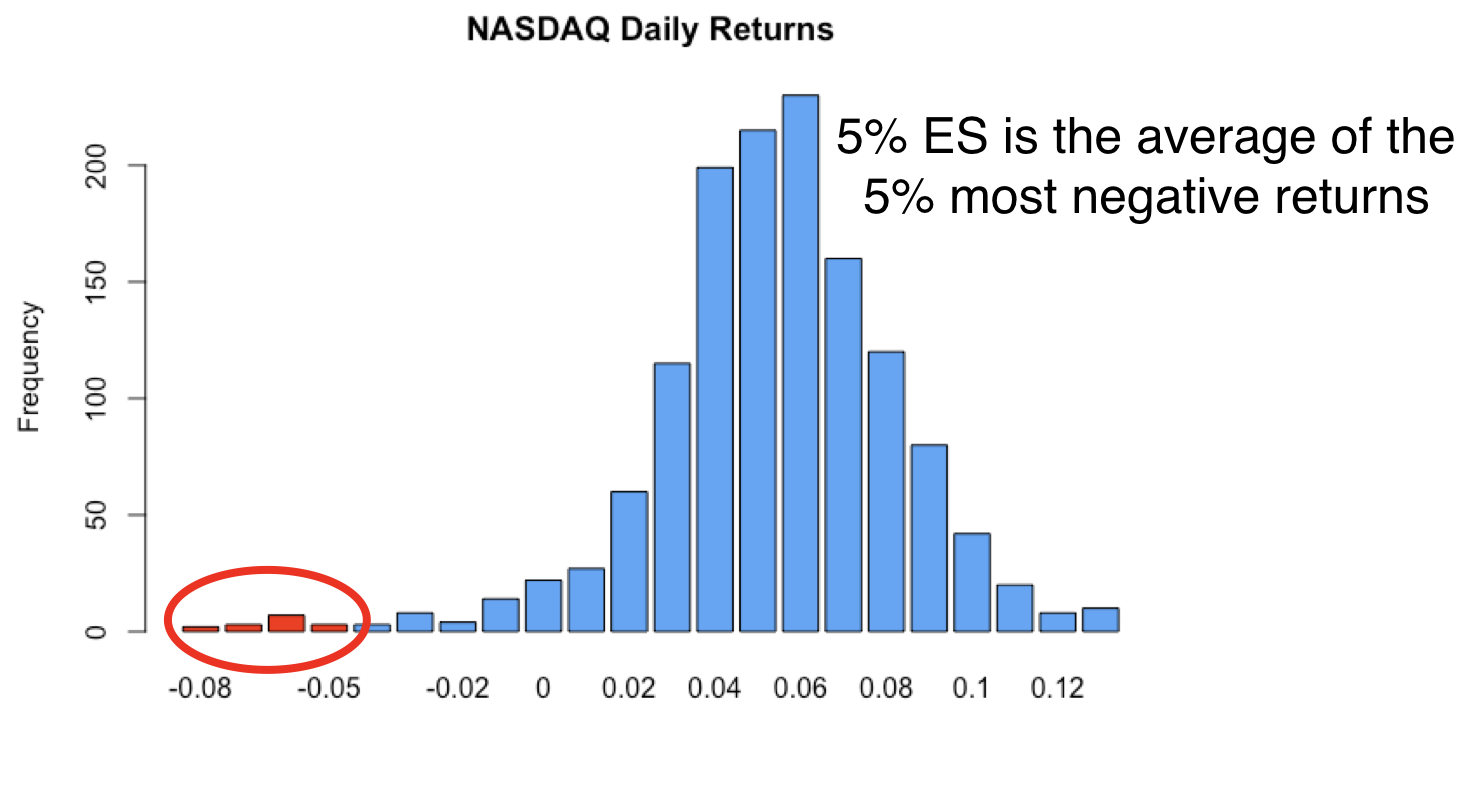
ch_2_video_4.017.png

Is it symmetric?
- Check the skewness
Are the tails fatter than those of the normal distribution?
- Check the excess kurtosis

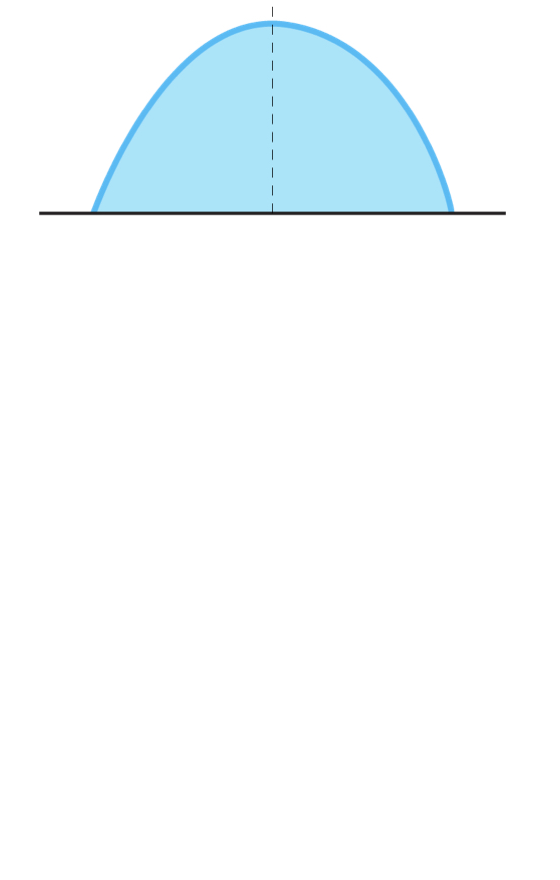
ch_2_video_4.024.png

Zero Skewness
- Distribution is symmetric
Negative Skewness
- Large negative returns occur more often than large positive returns

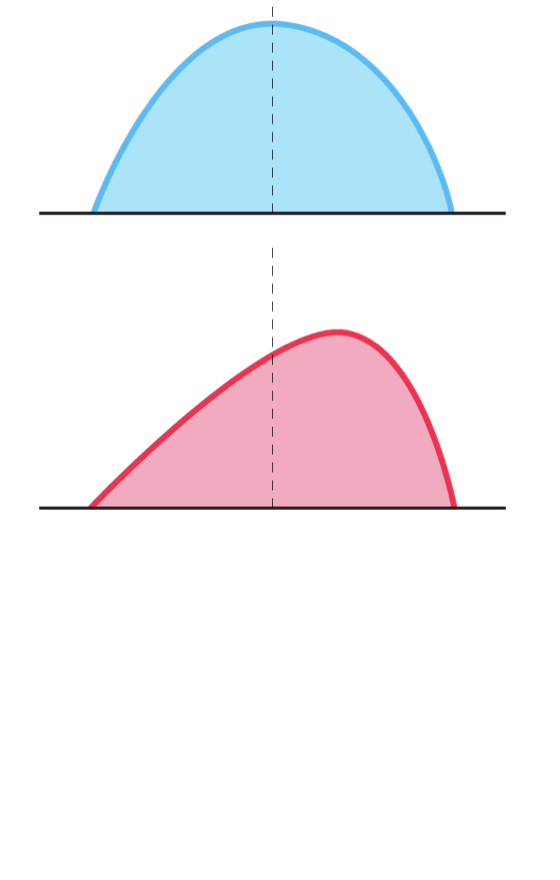
ch_2_video_4.025.png

Zero Skewness
- Distribution is symmetric
Negative Skewness
- Large negative returns occur more often than large positive returns
Positive Skewness
- Large positive returns occur more often than large negative returns

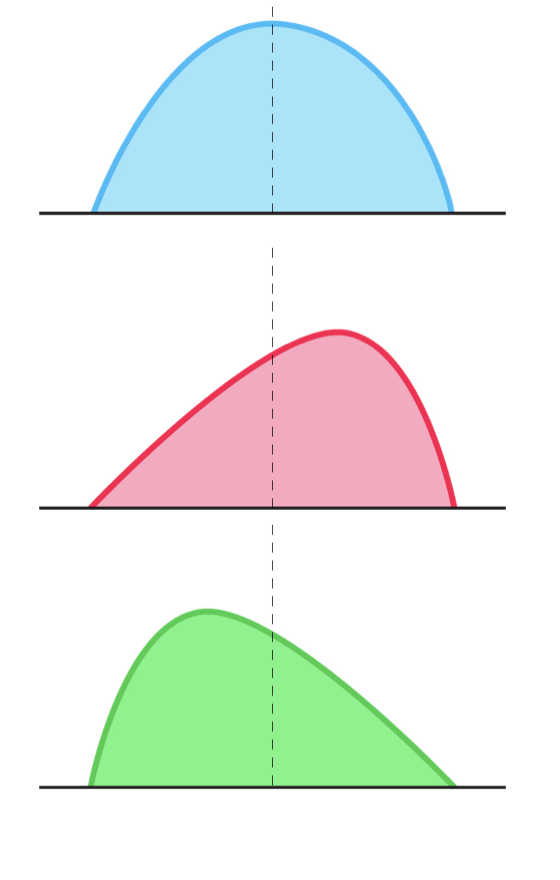
ch_2_video_4.026.png

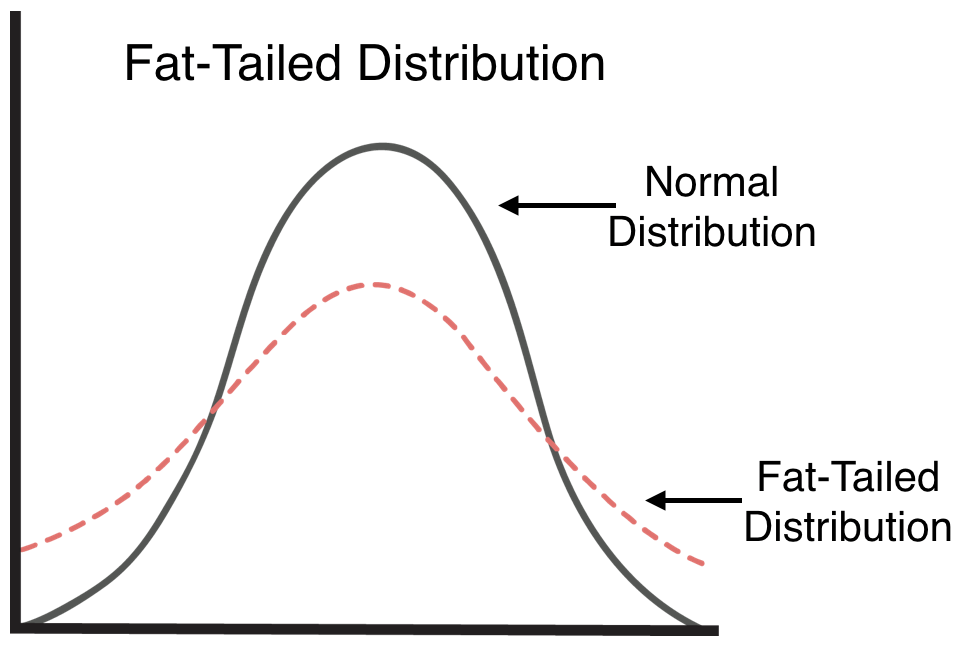
Screenshot 2019-08-21 at 12.01.32.png

Introduction to Portfolio Analysis in R