Using matrix notation
Introduction to Portfolio Analysis in R

Kris Boudt
Professor, Free University Brussels & Amsterdam
Variables at stake for n assets
$w$: the $N$ x 1 column-matrix of portfolio weights:
$$w = \left[{\begin{array}{c} w_1 \\ w_2 \\ ...\\w_N\end{array} }\right]$$
$\mu$: the $N$ x 1 column-matrix of expected returns:
$$\mu = \left[{\begin{array}{c} \mu_1 \\ \mu_2 \\ ...\\ \mu_N\end{array} }\right]$$
$R$: the $N$ x 1 column-matrix of asset returns:
$$ \color{red} {R =\left[{\begin{array}{c} R_1 \\ R_2 \\ ...\\R_N\end{array} }\right]}$$
$\Sigma$: The $N$ x $N$ covariance matrix of the $N$ asset returns:
$$w = \left[ {\begin{array}{cccc} {\large \sigma^2_{1}} & \sigma_{12} & ... & \sigma_{1N} \\ \sigma_{21} & {\large \sigma^2_{2}} & ... & \sigma_{2N} \\ ... & ... & ... & ... \\ \sigma_{N1} & \sigma_{N2} & ... & {\large \sigma^2_{N}} \end{array} } \right]$$
Generalizing from 2 to n assets
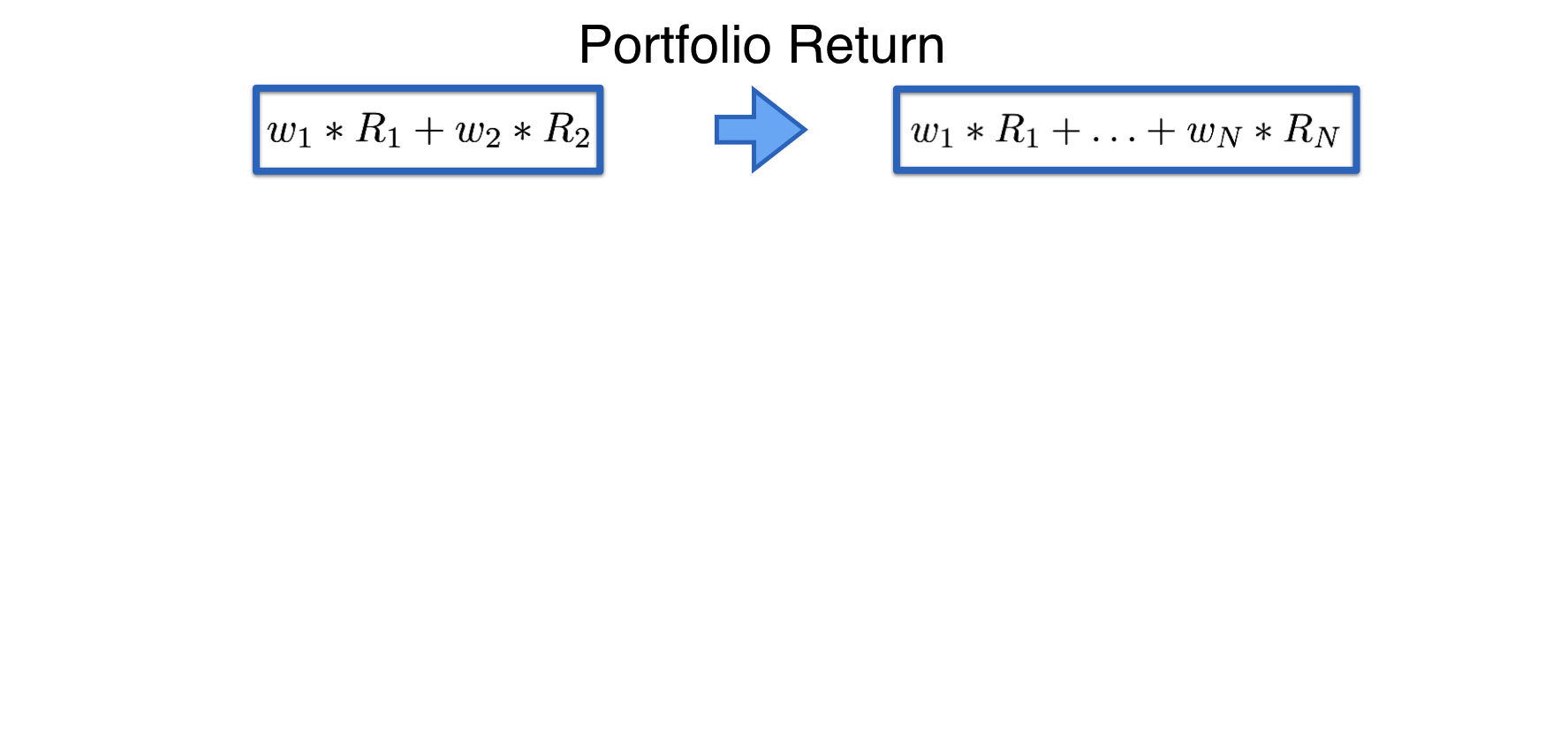
Generalizing from 2 to n assets
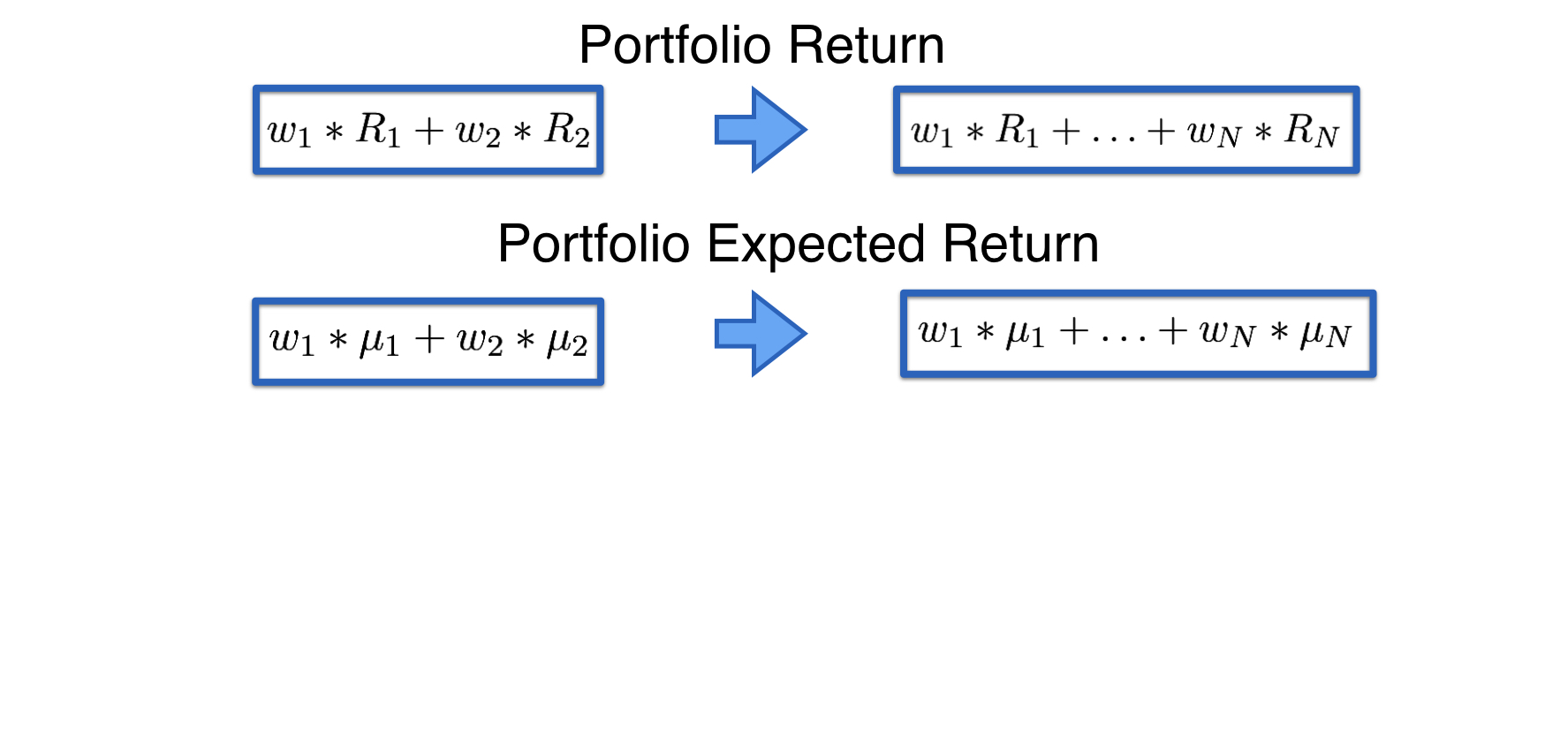
Generalizing from 2 to n assets
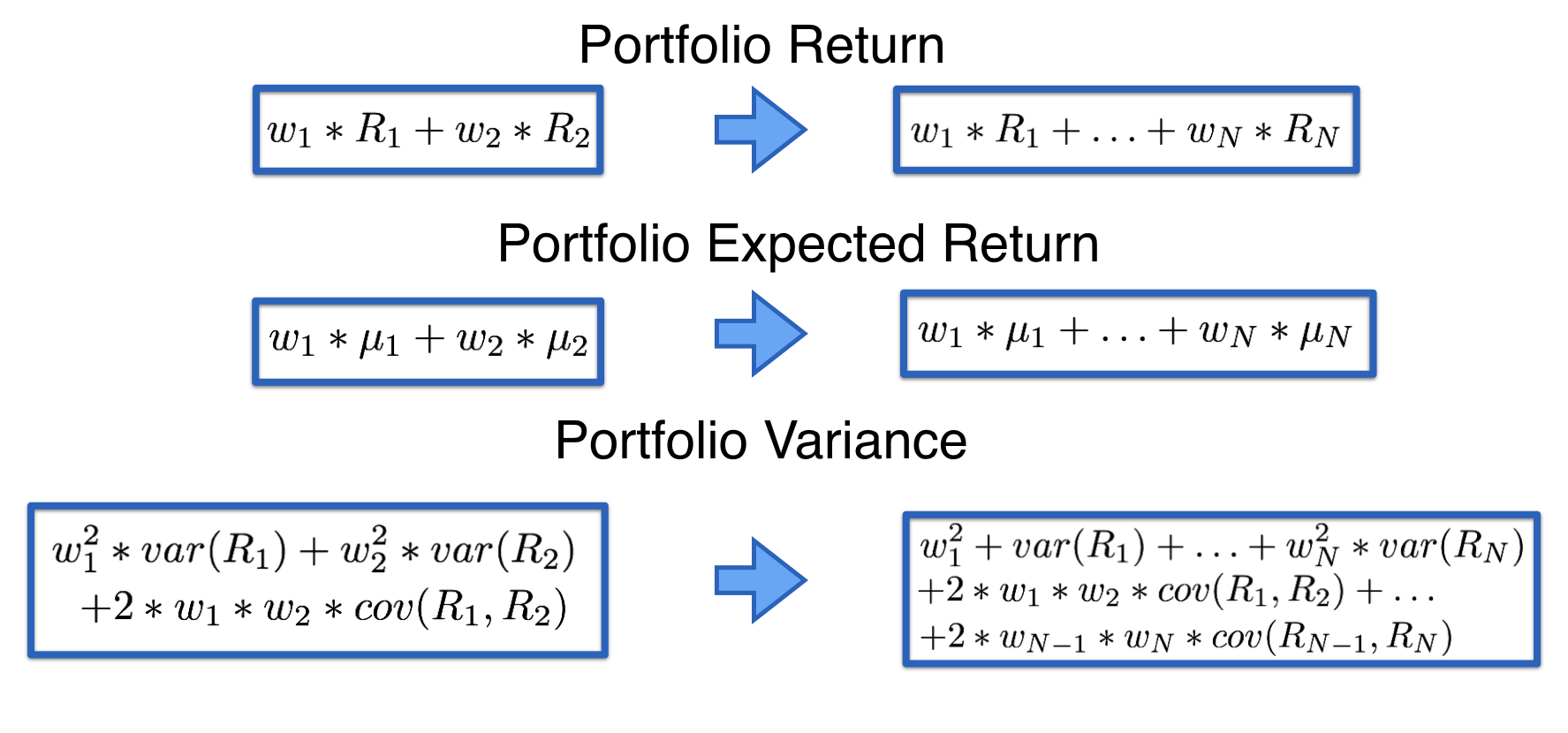
Matrices simplify the notation
- Avoid large number of terms by using matrix notation
- We have 4 matrices:
- weights ($w$), returns ($R$), expected returns ($\mu$), and covariance matrix ($\Sigma$)
$$w = \left[{\begin{array}{c} w_1 \\ w_2 \\ ...\\w_N\end{array} }\right]$$
$$w' = \left[{\begin{array}{c} w_1\ w_2\ ...\ w_N\end{array} }\right]$$
Simplifying the notation
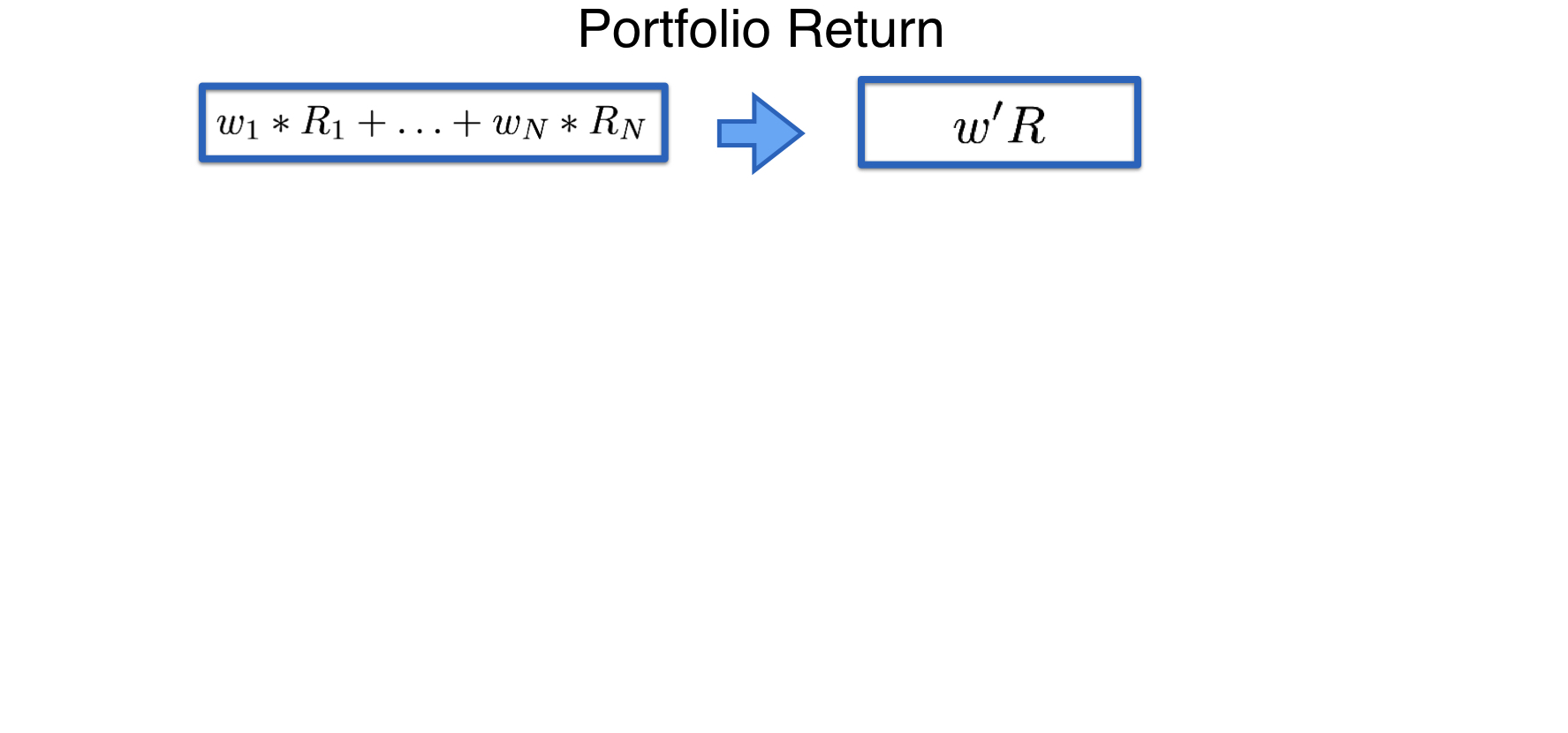
Simplifying the notation
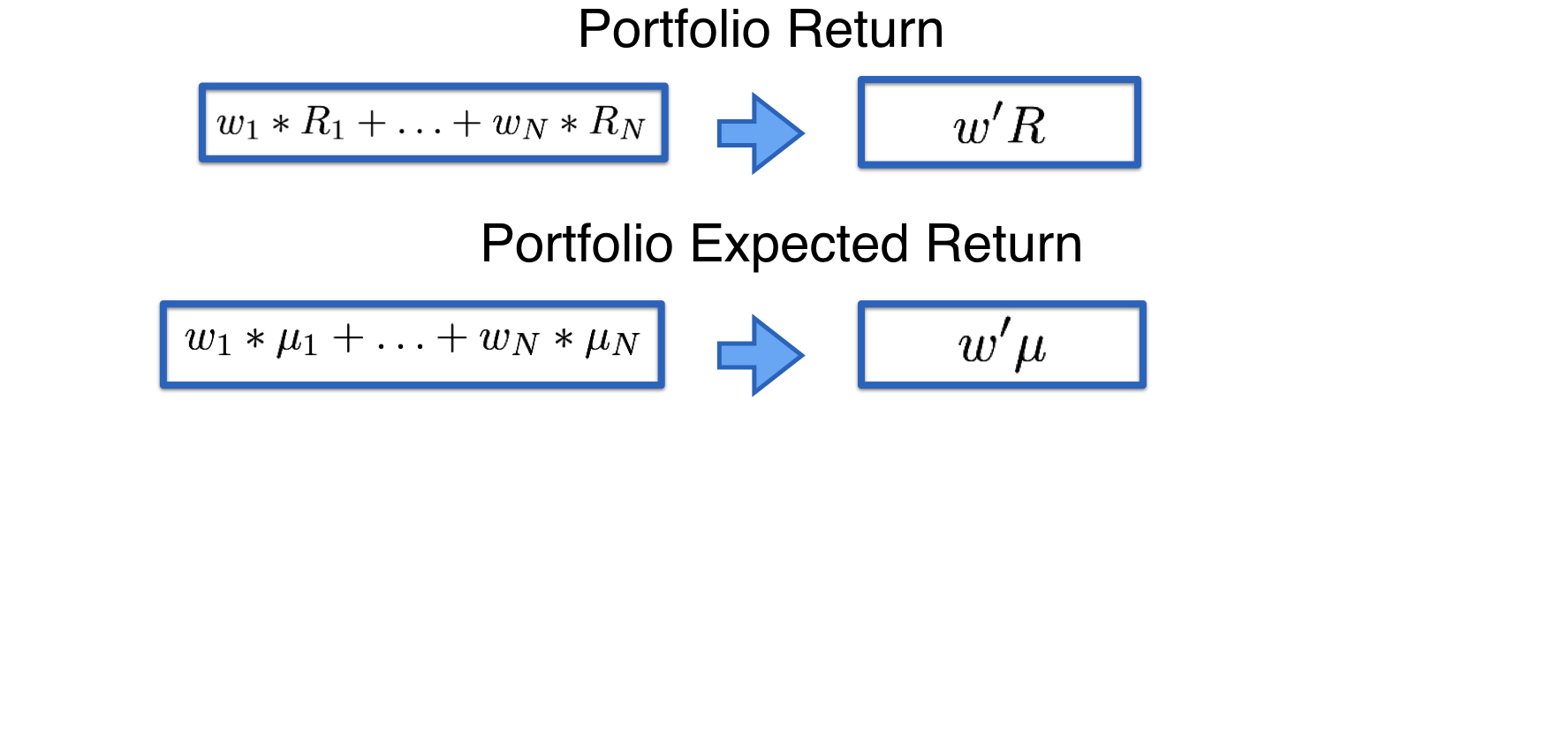
Simplifying the notation
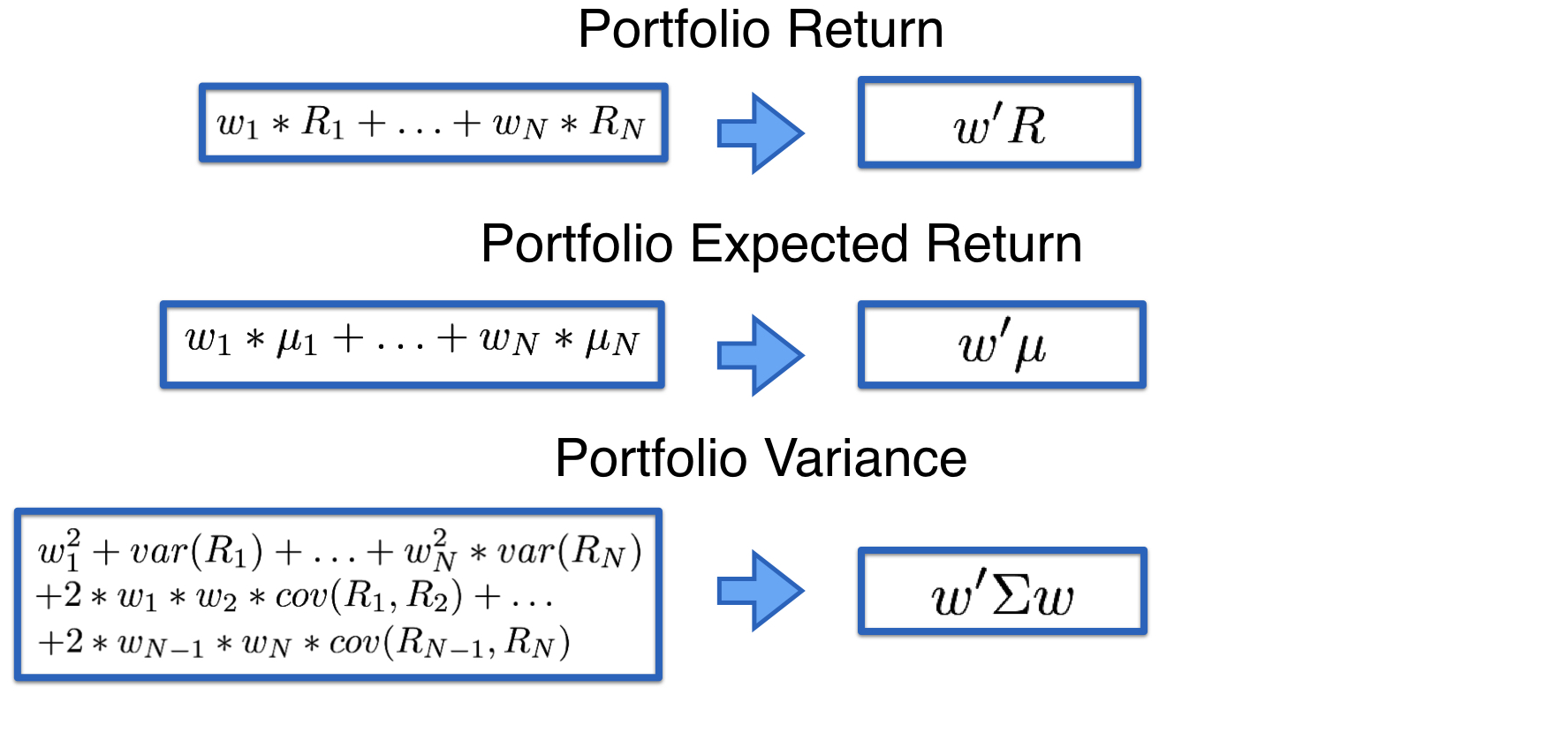
Let's practice!
Introduction to Portfolio Analysis in R

