Discrete distributions
Introduction to Statistics in R

Maggie Matsui
Content Developer, DataCamp
Rolling the dice

Rolling the dice
Choosing salespeople

Probability distribution
Describes the probability of each possible outcome in a scenario
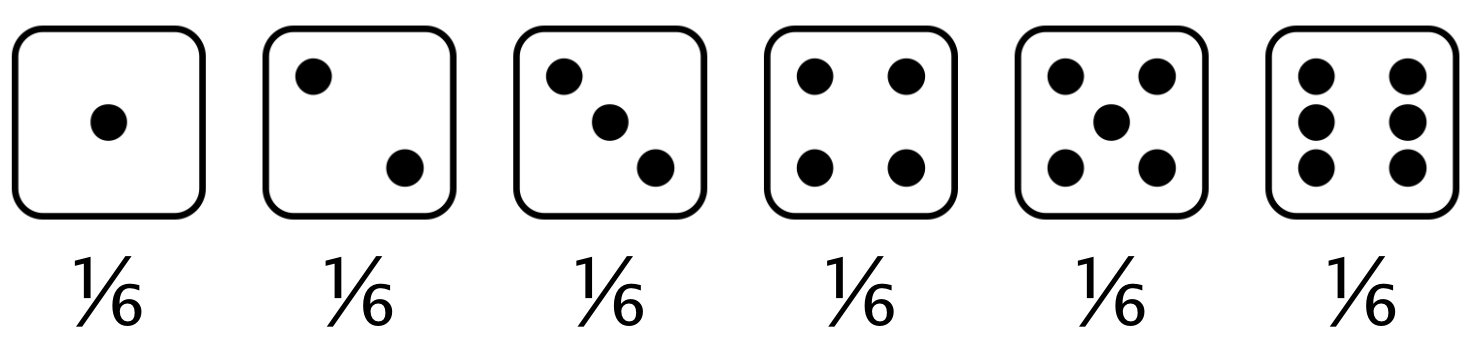
Expected value: mean of a probability distribution
Expected value of a fair die roll = $(1 \times \frac{1}{6}) + (2 \times \frac{1}{6}) +(3 \times \frac{1}{6}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3.5$
Visualizing a probability distribution
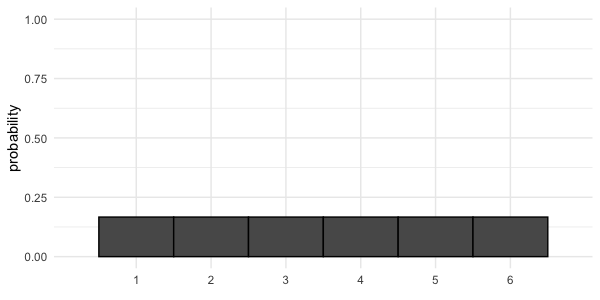
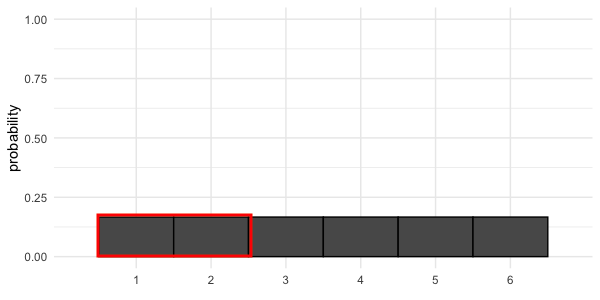
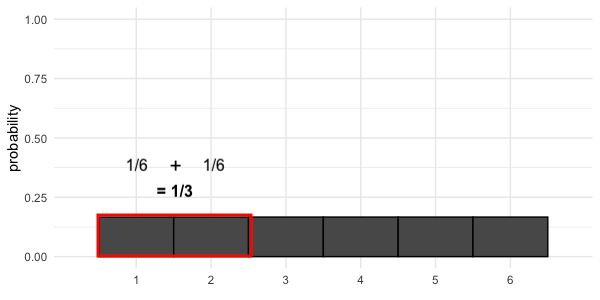
Probability = area
$$P(\text{die roll}) \le 2 = ~?$$
Probability = area
$$P(\text{die roll}) \le 2 = 1/3$$
Uneven die
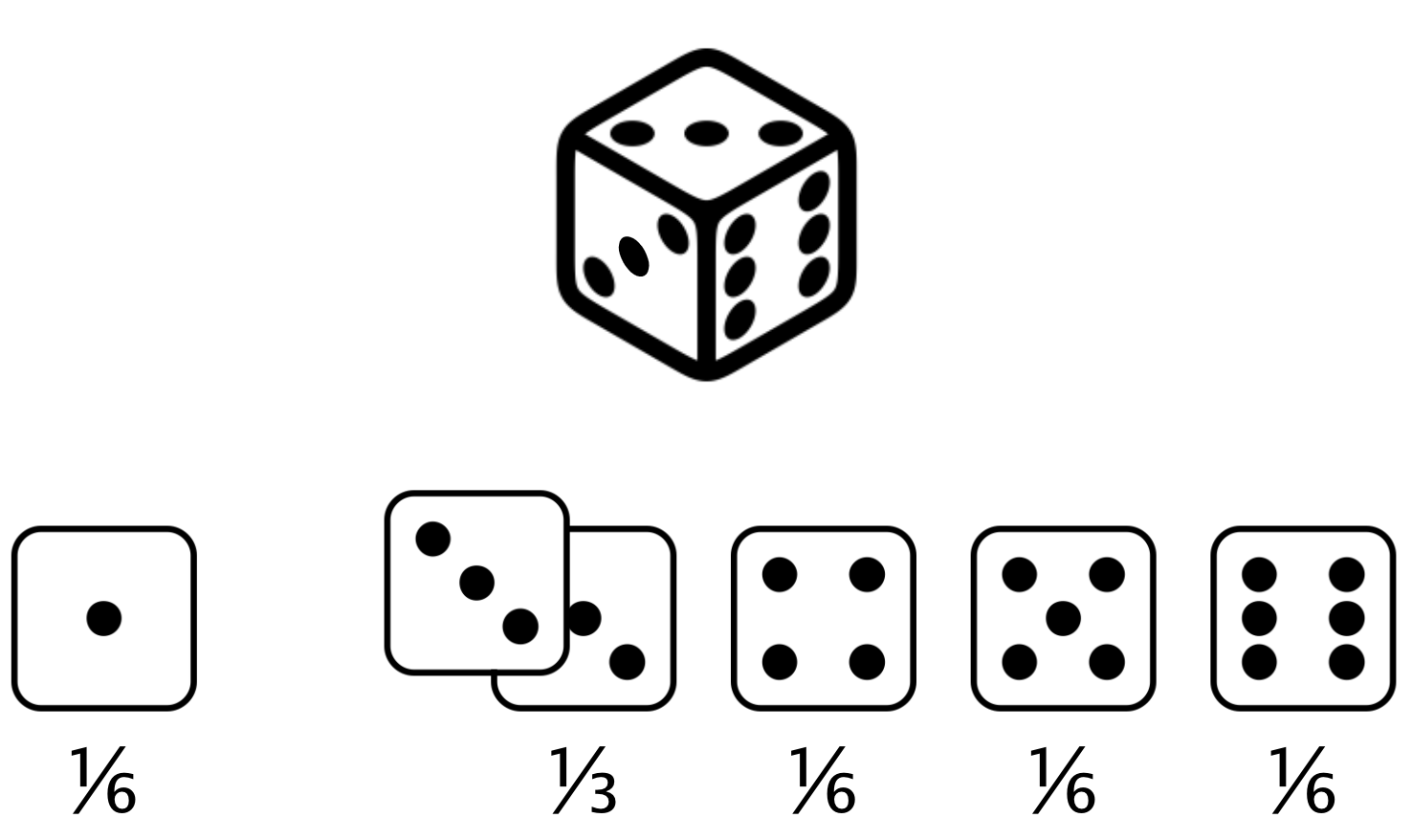
Expected value of uneven die roll = $(1 \times \frac{1}{6}) +(2 \times 0) +(3 \times \frac{1}{3}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3.67$
Visualizing uneven probabilities
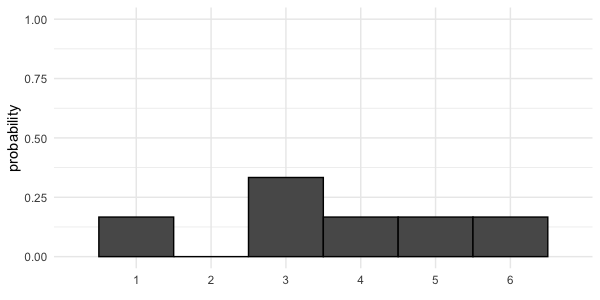
Adding areas
$$P(\text{uneven die roll}) \le 2 = ~?$$
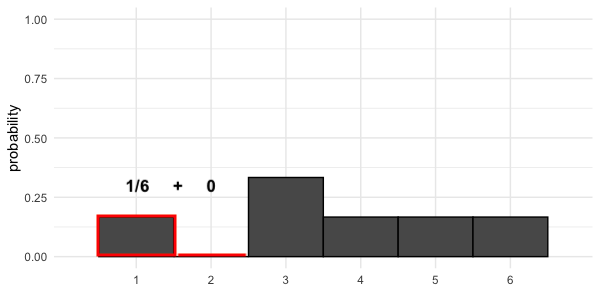
Adding areas
$$P(\text{uneven die roll}) \le 2 = 1/6$$

Discrete probability distributions
Describe probabilities for discrete outcomes
Fair die

Discrete uniform distribution
Uneven die
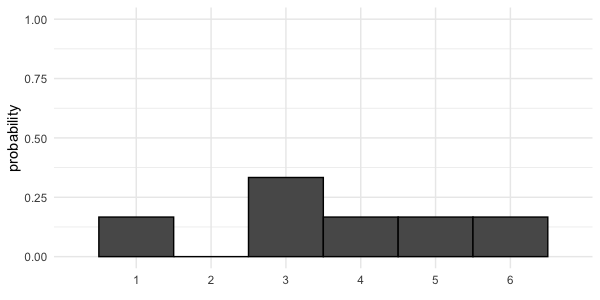
Sampling from discrete distributions
die
n
1 1
2 2
3 3
4 4
5 5
6 6
mean(die$n)
3.5
rolls_10 <- die %>%
sample_n(10, replace = TRUE)
rolls_10
n
1 1
2 1
3 5
4 2
5 1
6 1
7 6
8 6
...
Visualizing a sample
ggplot(rolls_10, aes(n)) +
geom_histogram(bins = 6)
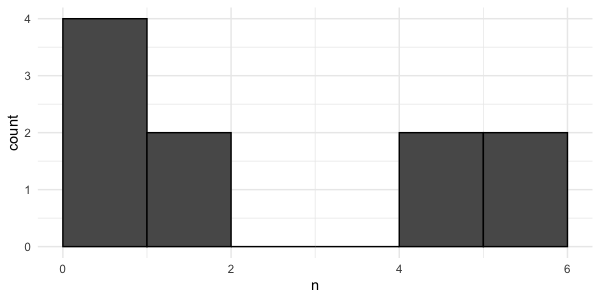
Sample distribution vs. theoretical distribution
Sample of 10 rolls
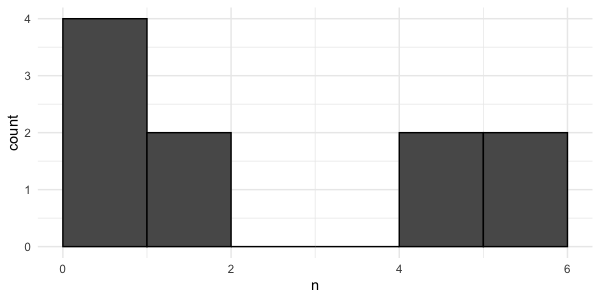
mean(rolls_10$n) = 3.0
Theoretical probability distribution

mean(die$n) = 3.5
A bigger sample
Sample of 100 rolls
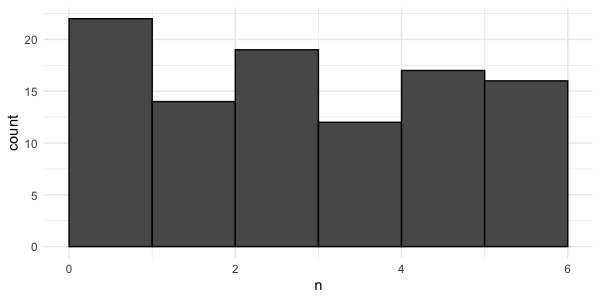
mean(rolls_100$n) = 3.36
Theoretical probability distribution

mean(die$n) = 3.5
An even bigger sample
Sample of 1000 rolls
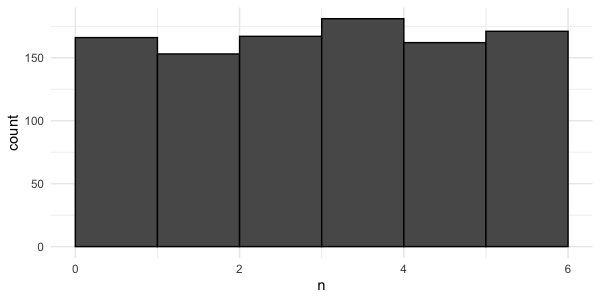
mean(rolls_1000$n) = 3.53
Theoretical probability distribution

mean(die$n) = 3.5
Law of large numbers
As the size of your sample increases, the sample mean will approach the expected value.
| Sample size | Mean |
|---|---|
| 10 | 3.00 |
| 100 | 3.36 |
| 1000 | 3.53 |
Let's practice!
Introduction to Statistics in R

