Multivariate skew distributions

Multivariate Probability Distributions in R

Surajit Ray

Reader, University of Glasgow

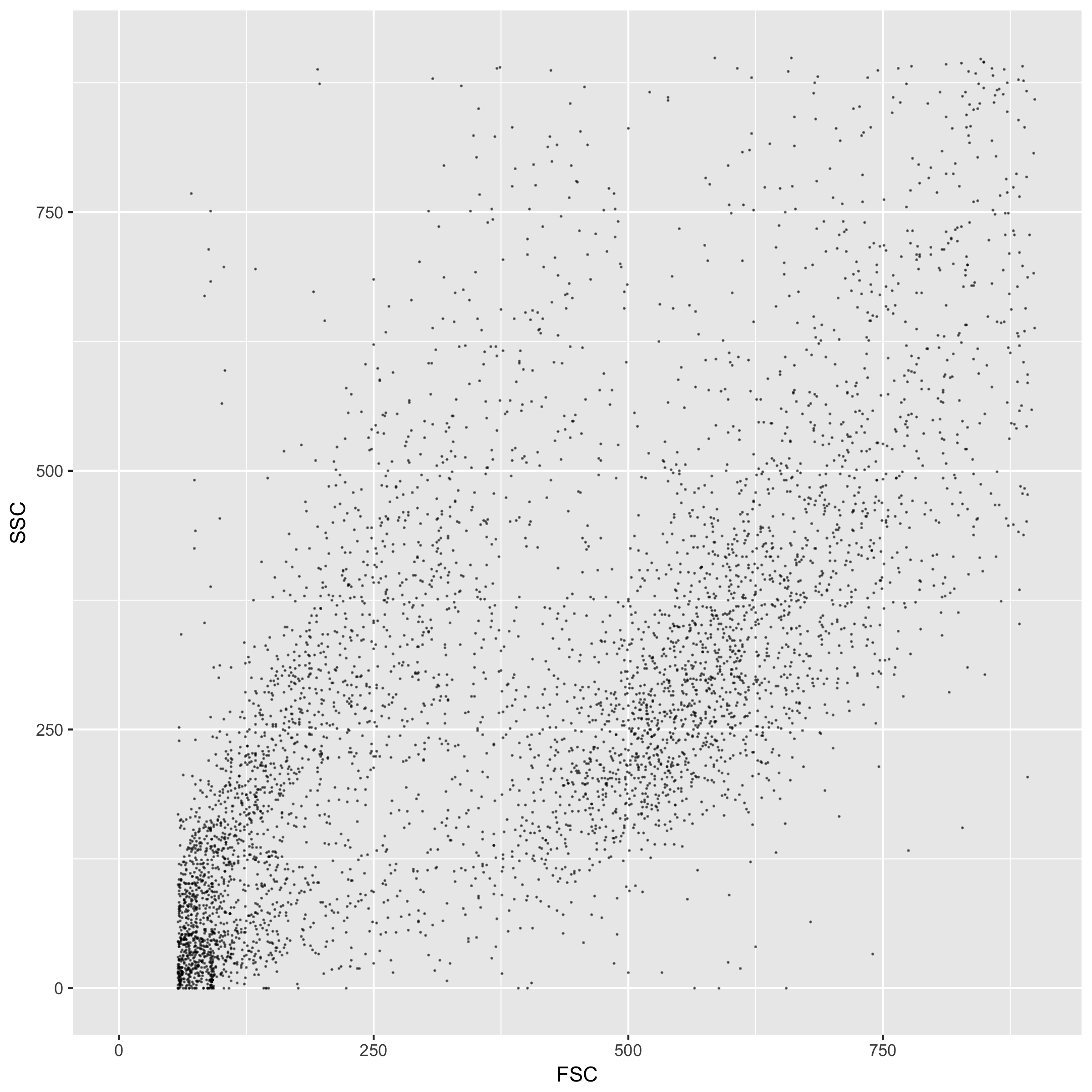
Skew multivariate distribution: scatterplot

Flow cytometry data -- side scatter (SSC) and forward scatter (FSC)

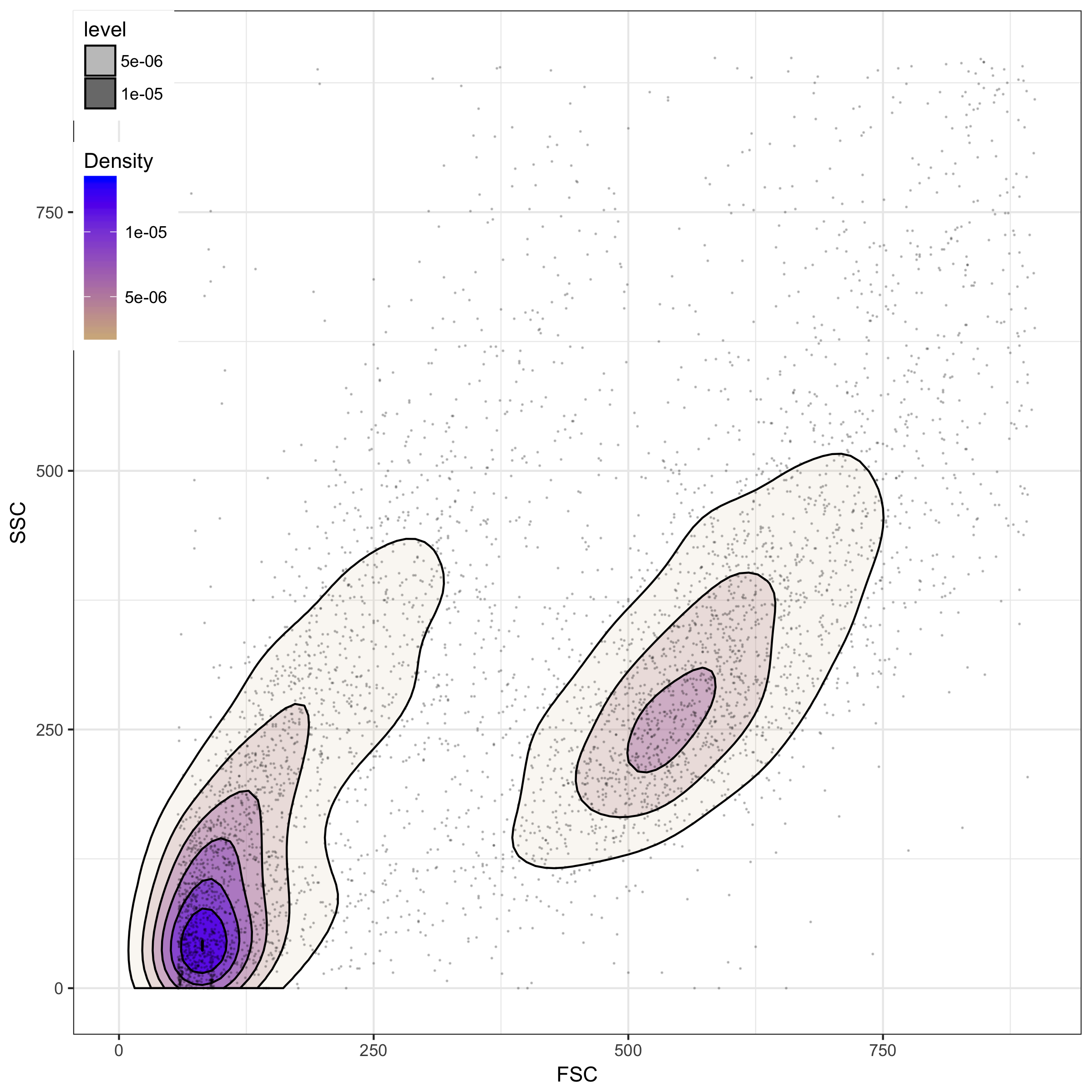
Skew multivariate distribution: contour plot

Flow cytometry data -- side scatter (SSC) and forward scatter (FSC)

Univariate skew-normal distribution

General skew-normal is denoted by $SN(\xi,\omega,\alpha)$

$\xi$ and $\omega$ are the location and scale parameters

Simplest form: $z \sim SN(\alpha) $

$\alpha$ is the skewness parameter

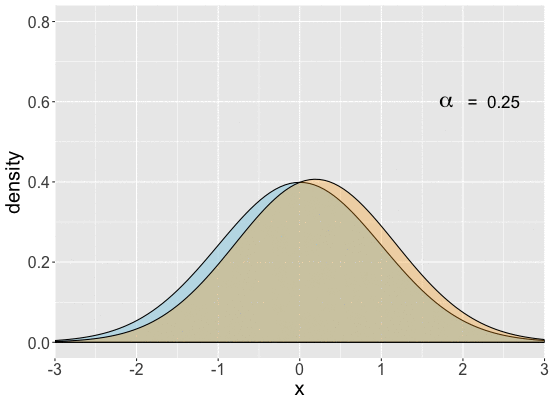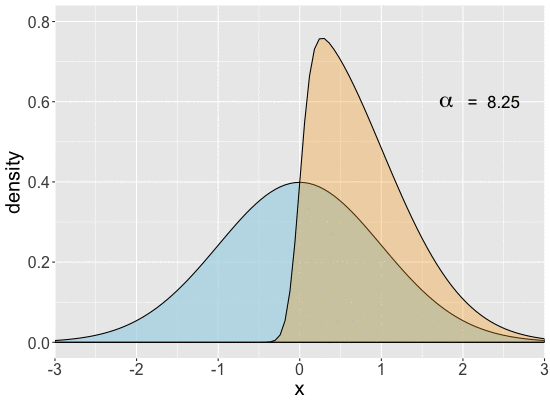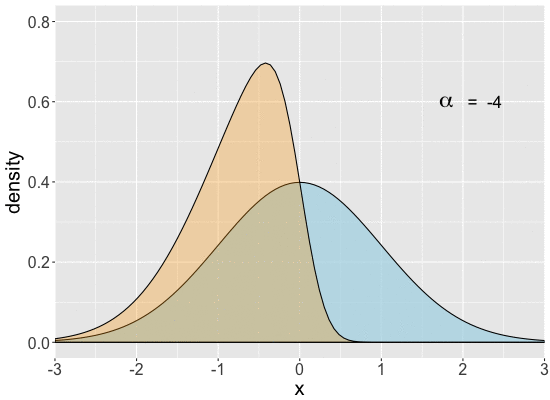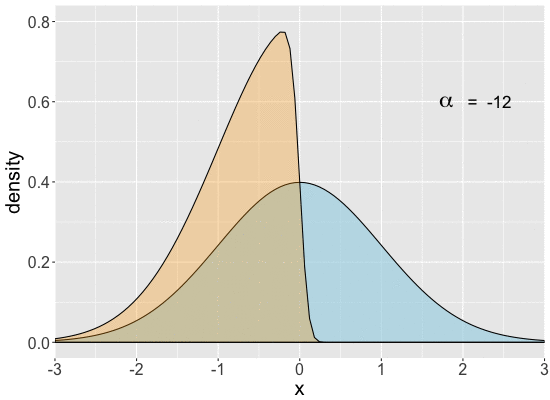
Range of univariate skew-normal distributions

Comparing $SN(\alpha)$ to a standard Normal

For $\alpha>0$ skewed to the right
For $\alpha<0$ skewed to the left
$SN(0)$ is the same as a standard Normal

Multivariate skew-normal distribution

Notations: three-dimensional multivariate skew-normal distribution

$SN(\xi,\Omega,\alpha)$

$\xi$ location parameter (vector of length $3$)
$\Omega$ variance-covariance parameter ($3 \times 3$ matrix)
$\alpha$ skewness parameter (vector of length $3$)

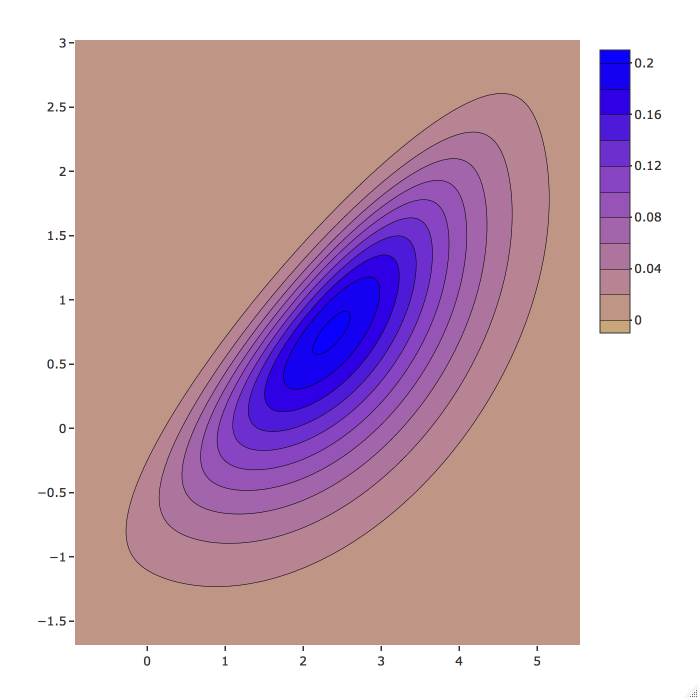
Bivariate skew-normal distribution contour plot

Bivariate skew-normal

${\xi}={\begin{pmatrix} 1 \\ 2 \end{pmatrix}},\quad { \Omega }={\begin{pmatrix} 1 & 0.5 \\ 0.5 & 2 \end{pmatrix}}$, ${\alpha}={\begin{pmatrix} -3 \\ 3 \end{pmatrix}}$.

Functions for skew-normal distribution

From sn library:

dmsn(x, xi, Omega, alpha)
pmsn(x, xi, Omega, alpha)
rmsn(n, xi, Omega, alpha)
- Need to specify xi, Omega, alpha

Functions for skew-t distribution

From sn library:

dmst(x, xi, Omega, alpha, nu)
pmst(x, xi, Omega, alpha, nu)
rmst(n, xi, Omega, alpha, nu )
- Need to specify xi, Omega, alpha, nu (degrees of freedom)

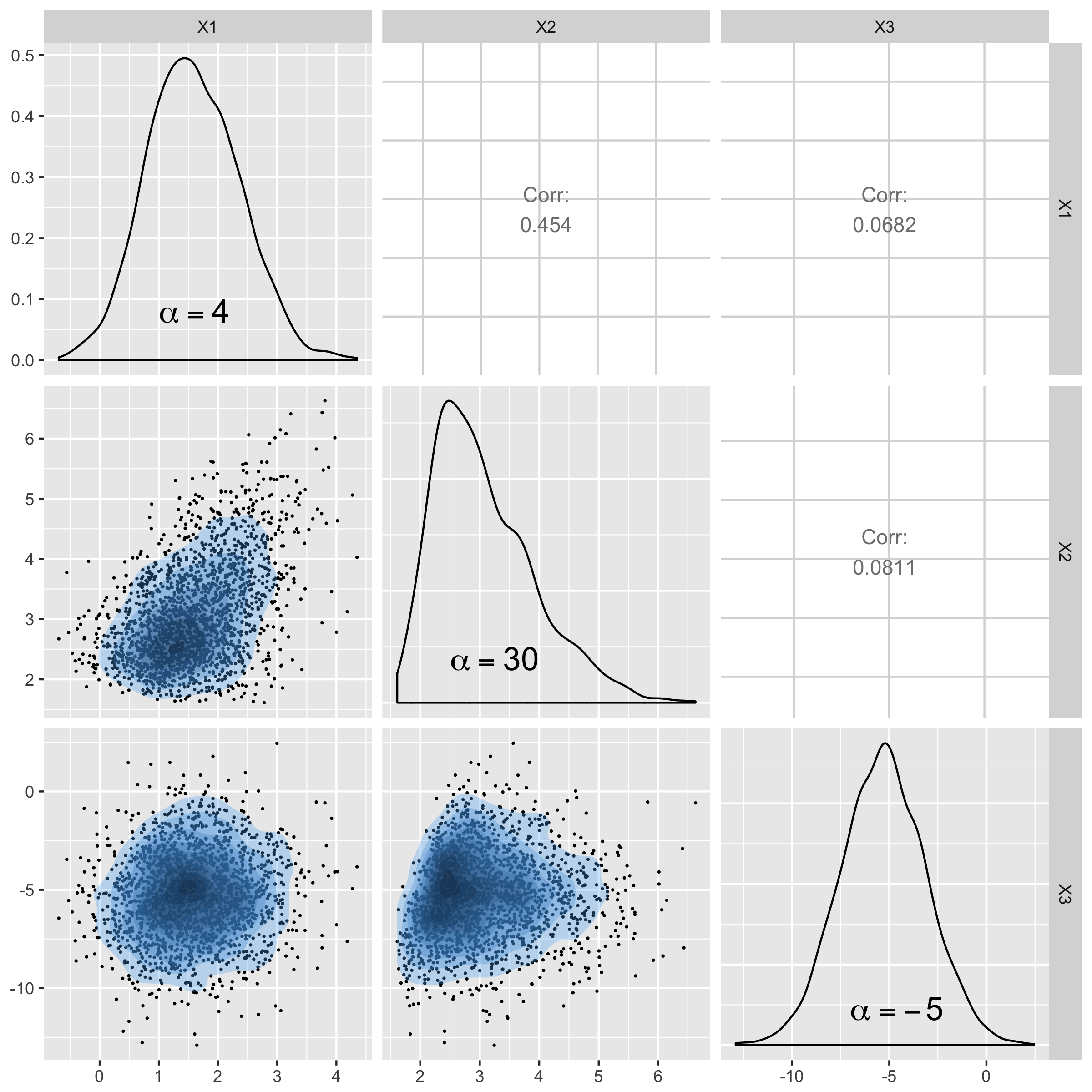
Generating skew-normal samples

Generate 2000 samples from 3 dimensional skew-normal

$ SN\left(\xi= \begin{pmatrix} 1 \\ 2 \\ -5 \end{pmatrix} , \Omega={\begin{pmatrix} 1 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & 0 & 5 \end{pmatrix}}, \alpha=\begin{pmatrix} 4 \\ 30 \\ -5 \end{pmatrix} \right)$

# Specify xi, Omega and alpha
xi1 <- c(1, 2, -5) 
Omega1 <- matrix(c(1, 1, 0,
                   1, 2, 0,
                   0, 0, 5), 3, 3)
alpha1 <- c(4, 30, -5)

# Generate samples
skew.sample <- rmsn(n = 2000, xi = xi1, Omega = Omega1, alpha = alpha1)

Sample from skew-normal distribution

Generating skew-t samples

Generate 2000 samples from 3 dimensional skew-t with

$\xi= \begin{pmatrix} 1 \\ 2 \\ -5 \end{pmatrix} , \Omega={\begin{pmatrix} 1 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & 0 & 5 \end{pmatrix}}, \alpha=\begin{pmatrix} 4 \\ 30 \\ -5 \end{pmatrix}, df = 4$

# Generate samples
skewt.sample <- rmst(n = 2000, xi = xi1, Omega = Omega1, alpha = alpha1, nu = 4)

Estimation of parameters from data

Need iterative algorithm to estimate the parameters of a skew-normal distribution
- No explicit equation to calculate parameters
Several functions in sn package, including msn.mle() function

Estimation of parameters from data

msn.mle(y = skew.sample, opt.method = "BFGS")

$dp
$dp$beta
        X1    X2    X3
[1,] 1.024 2.021 -4.81

$dp$Omega
        X1      X2      X3
X1  0.9154  0.8865 -0.1507
X2  0.8865  1.8276 -0.3560
X3 -0.1507 -0.3560  5.0352

$dp$alpha
    X1     X2     X3 
 3.670 28.465 -5.029

Samples were generated using:

$\xi= \begin{pmatrix} 1 \\ 2 \\ -5 \end{pmatrix} , \Omega={\begin{pmatrix} 1 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & 0 & 5 \end{pmatrix}}, \alpha=\begin{pmatrix} 4 \\ 30 \\ -5 \end{pmatrix} $

Now let's do some exercises with skew-normal distributions!

Multivariate Probability Distributions in R